Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 80
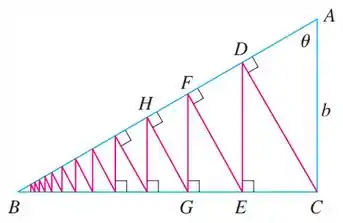
É dado um triângulo com e . é desenhado perpendicularmente a , é desenhado perpendicularmente a , , e esse processo continua indefinidamente, como mostrado na figura. Calcule o comprimento total de todas as perpendiculares
Em termos de e .
Passo 1
E aí, galerinha? Essa questão só parece difícil, vamos ver passo a passo que ela só “assusta”:
O que vamos precisar fazer aqui é achar uma expressão que traz a soma desses seguimentos perpendiculares. Achando a soma, vamos ter esse comprimento total, que nada mais é que somar cada uma dessas perpendiculares e entender para qual valor elas se aproximam.
Sempre que o enunciado traça uma reta, dá pra ver na imagem que ela forma um novo triangulo reto. Podemos ver também que essa nova reta é sempre oposta ao ângulo .
Vamos usar isso pra começar a achar a sequência do comprimento das retas, que vou chamar de , então a gente tá buscando
Vamos ter que procurar uma fórmula para e para isso vamos calcular alguns primeiros termos e identificar os padrões que esse cálculo segue.
Passo 2
Pensando no primeiro triangulo
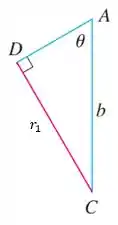
Temos que é oposto ao ângulo , e que a hipotenusa é , utilizando a fórmula do seno, cateto oposto sobre hipotenusa
Isolando
Para o segundo triangulo
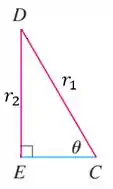
Temos oposto a novamente e a hipotenusa é , com a mesma relação
Substituindo
E dessa forma vai seguir, o próximo triangulo vai ter hipotenusa , então
Passo 3
Agora precisamos olhar nossos termos ali do Passo 2 e identificar o padrão que seguem para acharmos o termo geral para
Então, de forma geral:
E a nossa série tem a cara:
Passo 4
Essa série tem a cara de uma geométrica, basta manipular
E essas séries nós conseguimos achar um valor para , neste caso , e como o ângulo está , porque se for maior que não conseguimos um triangulo reto e igual a não é possível pois o outro ângulo já é reto e não conseguiríamos fechar o triangulo e se for igual a , não teríamos triangulo. Neste intervalo o seno vale entre , portanto e a série converge para