Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 3.10 - Ex. 21

Dados x e d x = ∆ x , calcule d y   e   ∆ y . Depois, mostre em um diagrama a reta tangente.

x = 3 ; d x = 0,8

y = x - 2

Passo 1

Fala aí pessoal, partiu resolver mais um problema de cálculo.

Nessa questão nos é dado um ponto x e um d x .

x = 3 ; d x = 0,8

Além de uma função:

y = x - 2

Pede para considerarmos que d x = Δ x .

Por fim, ela pede para a gente mostrar em um diagrama a reta tangente.

Bom, para calcular ∆ y ,   vamos ter que usar:

∆ y = f x + ∆ x - f x

Já para achar d y , podemos usar que a diferencial é dada por:

d y = f ' x d x

Ou seja, vamos precisar encontrar a derivada dessa função.

Passo 2

Primeiramente encontrando Δ y , temos:

∆ y = f x + ∆ x - f x

∆ y = f 3,8 - f ( 3 ) = 0,34

Agora, para achar d y , vamos usar:

d y = d x × f ' x

Nossa função é:

f x = x - 2

Sua derivada é portanto, usando a regra da cadeia:

f ' x = d x - 2 d x - 2 ⋅ d x - 2 d x

Para derivar a raíz fazemos:

x ' = 1 2 x

Dessa forma, temos:

f ' x = 1 2 x - 2 1

Substituindo x = 3 , temos:

f ' 3 = 1 2 3 - 2 = 1 2

Agora substituindo no d y , chegamos em:

d y = f ' x d x

d y = 1 / 2 ⋅ 0,8 = 0,4

Passo 3

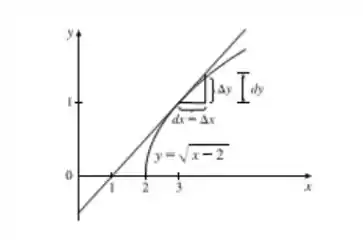
Para desenhar um diagrama, você deve traçar a função x - 2 , que é igual a função x só que transladada em 2 unidades para a direita.Depois disso, vai traçar a reta tangente em x = 3 .

E então formar um triângulo de base d x = Δ x e de altura igual a d y que vai até a reta tangente e Δ y que vai até a função.

Resposta

∆ y = 0,34

d y = 0,4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ponto P ( 2 , - 1 ) está sobre a curva y = 1 1 - x .Se Q é o ponto x , 1 1 - x , use sua calculadora para determinar a inclinação da reta secante P Q , com precisão de seis casas decimais, para os s
O ponto P ( 0,5 ; 0 ) está sobre a curva y = cos ⁡ π x .Se Q é o ponto x , cos ⁡ π x , use sua calculadora para determinar a inclinação da reta secante P Q , com precisão de seis casas decimais, para
61. Ache uma função cúbica y = a x 3 + b x 2 + c x + d cujo gráfico tem tangentes horizontais nos pontos ( - 2,6 ) e ( 2,0 )
37-38 Estime o valor de f ' ( a ) dando um zoom no gráfico de f . Depois derive a f e determine o valor exato de f ' ( a ) e compare com a sua estimativa.37. f ( x ) = 3 x 2 - x 3,a = 1
41-42 Ache uma equação da reta tangente à curva no ponto dado. Ilustre fazendo o gráfico da curva e a reta tangente sobre a mesma tela;42. y = x x ( 4,8 )