Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 3.10 - Ex. 20

Dados x e d x = ∆ x , calcule d y   e   ∆ y . Depois, mostre em um diagrama a reta tangente.

x = 0 ;   d x = - 0,3

y = x - x ³

Passo 1

Fala aí pessoal, partiu resolver mais um problema de cálculo!

O enunciado pediu pra gente encontrar a diferencial d y e a variação Δ y , dados x e d x = Δ x .

Para calcular ∆ y ,   vamos precisar usar a fórmula:

∆ y = f x + ∆ x - f x

Depois, vamos substituir f x = x - x 3 , para x = 0 e d x = - 0,3 de modo que a gente consiga obter o valor de Δ y .

Além disso, vamos calcular o valor da diferencial, usando a definição:

d y = f ' x ∙ d x

Onde f ' ( x ) é a derivada da função y = x - x 3 .

Vamos lá!

Passo 2

Sabemos que para calcular ∆ y ,   vamos ter que usar:

∆ y = f x + ∆ x - f x

Mas d x = ∆ x e temos d x = - 0,3 e x = 0 . Então, vamos ficar com:

∆ y = f 0 + - 0,3 - f 0

∆ y = f - 0,3 - f 0

Só que f - 0,3 = - 0,3 - 0,3 3 e f 0 = 0 . Logo, teremos:

∆ y = - 0,3 - - 0,3 3 - 0

Resolvendo:

∆ y = - 0 , 2 7 3

Passo 3

Agora, para achar d y , vamos usar:

d y = f ' x ∙ d x

Calculando a derivada de y = x - x 3 , temos f ' x = 1 - 3 x 2 . Então, substituindo na expressão, vamos ter:

d y = 1 - 3 x 2 ∙ d x

Em x = 0 , essa derivada nos fornece f ' 0 = 1 . Além disso, temos d x = - 0,3 . Logo, teremos:

d y = 1 ∙ ( - 0,3 )

d y = - 0,3

Agora representando a reta tangente no ponto x = 0 , junto coma nossa função y = x - x 3 , temos:

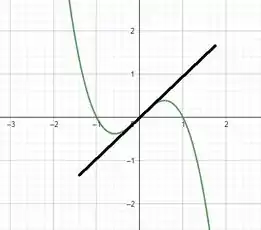
Valeu, galera! Até a próxima! 😉

Resposta

∆ y = - 0,273

d y = - 0,3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

51. A reta normal à curva C em um ponto P é, pela definição, a reta que passa por P e é perpendicular à reta tangente a C em P. Ache uma equação da reta normal à parábola y = 1 - x 2 no ponto 2 , - 3
21-24. Encontre uma equação da reta tangente à curva dada no ponto especificado.21. y = tan ⁡ x , π 4 , 1
25.(a) Encontre uma equação da reta tangente à curva y = x c o s x no ponto ( π , - π ) (b) Ilustre a parte (a) fazendo o gráfico da curva e a reta tangente na mesma tela.
O gráfico ilustra a função posição de um carro. Use a forma do gráfico para explicar suas respostas para a seguinte questão.Qual a velocidade inicial do carro?O carro está mais rápido em B ou C?O carr
Esboce o gráfico de uma função g que é continua no domínio ( - 5,5 ) e onde g 0 = 1 ,g ' 0 = 1 ,g ' - 2 = 0 , lim x → - 5 + ⁡ g ( x ) = ∞ e lim x → 5 - ⁡ g ( x ) = 3 .