Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 62
Dados os pontos e , encontre o ponto do intervalo do eixo que maximize o ângulo .
Passo 1
Então galera, a fim de facilitar nossa visualização do problema esboçamos os pontos , e o ponto , além dos ângulos e triângulos retângulos formados por esses pontos, ok? O esboço ficou assim ó:
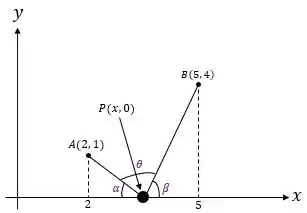
O enunciado pede para que maximizemos o ângulo da figura. Para determinarmos uma expressão para devemos encontrar as expressões de e também, então vamos nessa!
Passo 2
O ângulo pode ser expresso da seguinte forma:
Mas quem seriam as expressões de e ? Olhando para o triângulo retângulo formado pelo ponto na figura, temos:
Logo:
Agora olhando para o triângulo retângulo formado pelo ponto na figura, temos:
Logo:
Então a expressão de será:
Que é uma expressão em função de , como o enunciado pede! Show!
Passo 3
Como queremos maximizar esse ângulo, então vamos utilizar os conceitos que aprendemos no cálculo! Derivando nossa função:
Simplificando, teremos:
Agora igualando a zero:
A única forma disso resultar em zero é se:
Utilizando Bháskara, teremos:
E esses são nossos pontos críticos, galera!
Passo 4
Aqui vale ressaltar uma coisa, pessoal. Pela figura do passo 1 temos que nosso intervalo é , certo? Então nosso único ponto crítico mesmo será:
Mas como fazemos pra saber se esse ponto é, de fato, um valor de que maximiza nosso ângulo? Se pegarmos um valor menor que teremos:
E se pegarmos um valor maior que teremos:
Como a derivada passa de crescente para decrescente, isso implica que é um ponto de máximo mesmo!
E está aí nossa resolução, galera! 😉
Resposta
Ponto: .