Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 58
Um homem está sentado em um barco a da margem (reta) de um lago. Uma cidade está localizada nessa margem a do ponto da margem do lado que está mais próximo do homem. Ele pretende remar em linha reta até um ponto na margem oposta e depois caminhar o restante ao longo da margem (Figura Ex-58). Para que ponto ele deve remar a fim de chegar a seu destino no menor tempo se ele:
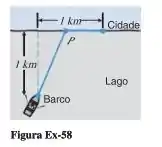
a) pode andar a e remar a ?
b) pode andar a e remar a ?
Passo 1
a) Então galera, a fim de facilitar nossa visualização vamos desenhar a rota do barco, tudo bem? Teremos algo assim:
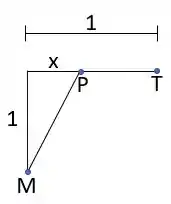
Vale ressaltar que os valores foram dados pelo enunciado, ok? Não tem nada de novo aqui! O que temos que determinar aqui é uma expressão para o tempo em que o homem leva para sair do lado e chegar até a cidade, ou seja, para sair do ponto e chegar até o ponto . O tempo total será:
No qual é o tempo para ir de até e é o tempo para ir de até . Então bora que bora determinar essas equações!
Passo 2
Da cinemática temos que a velocidade média de um corpo é dada da seguinte forma:
Para , no qual o homem rema:
Substituindo os valores que temos:
Para , no qual o homem caminha:
Substituindo os valores que temos:
Então o tempo total será:
Passo 3
Como queremos saber os valores de para que o tempo seja mínimo, então temos que utilizar os conceitos de cálculo que aprendemos! Derivando nossa função, teremos:
Igualando a zero:
Elevando ambos os lados ao quadrado:
Então esse é nosso ponto crítico!
Passo 4
Agora que encontramos nosso ponto crítico, vale ressaltar que nosso intervalo é , pois é a distância máxima dos locais dado pelo enunciado! Sendo assim, temos que substituir os valores do intervalo e o ponto crítico que encontramos na nossa função original, a fim de determinarmos o valor de que minimiza o tempo, se liga:
Sendo assim, temos que a distância que minimiza o tempo é:
Passo 5
b) Para resolvermos essa parte devemos seguir os mesmos passos da letra anterior, galera! A diferença é que ele irá remar a agora, e não a . Sendo assim:
Derivando e igualando a zero:
Opa, aqui temos um problema! Conforme vimos no passo 4, nosso intervalo é e está FORA do intervalo! Sendo assim, a distância que minimiza o tempo, de acordo com o que calculamos no passo 4, é:
E essa é a nossa resolução, pessoal! 😉
Resposta
a) Distância que minimiza o tempo: ;
b) Distância que minimiza o tempo: .