Dar a fronteira dos seguintes subconjuntos do . Representar graficamente.
Passo 1
Olha, gente, a definição que o livro deu de fronteira é bem engraçada, falando das bolas abertas e não sei o que mais. Aqui a gente mexe é com a prática, e na prática, o que a gente vai ter que ver é a bordinha da função. A equação da bordinha vai ser a fronteira! E essa equação a gente obtém simplesmente trocando esses sinais de desigualdade e trocando por uma igualdade, assim, ó: reescrevendo o nosso conjunto...
A fronteira dele vai ser a equação:
Que é a equação de uma hipérbole equilátera de centro em . Temos que considerar também o eixo dos como fronteira, já que a hipérbole tem assíntota nesse eixo.
Passo 2
Pra ilustrar, olha como é o subconjunto:
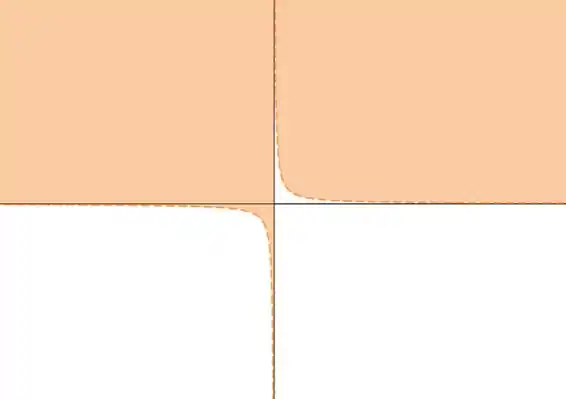
Pegou a idéia da fronteira?
Resposta
Hipérbole equilátera de centro em e o eixo .