Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 34
- Deduza a Equação para a óptica gaussiana da Equação 1 aproximando na equação 2 por seu polinômio de Taylor de grau 1.
- Mostre que se for trocado por seu polinômio de Taylor de grau 3 na equação 2, então a equação 1 se torna a equação 4 para a óptica de terceira ordem.
[Sugestão: Use os primeiros dois termos na série binomial para e . Além disso, use ]
Passo 1
E aí, galerinha! Tranquilo?
Primeira coisa: vamos colocar aqui no passo 1 todas as equações que essa questão tá falando.
Equação 1:
Equação 2:
Equação 3:
Equação 4:
A parte a) pede pra gente deduzir a equação 3 para a equação 1, aproximando na equação 2 por seu polinômio de Taylor de grau 1:
A aproximação de por seu polinômio de Taylor de grau 1 é simplesmente:
Então, basicamente vamos pegar a equação 2, e achar os valores de e usando . Depois aplicamos na equação 1 até chegarmos na equação 3.
A parte b) pede para mostrarmos que trocando por seu polinômio de Taylor de grau 3 na equação 2, transformamos a equação 1 na equação 4. Para isso vamos precisar considerar:
E usarmos a série binomial para achar e :
Então precisamos achar esse polinômio dado por:
Vamos juntos!
Passo 2
Usando a aproximação linear para , ou seja, usando
Temos, das equações 2:
Fatorando o termo e rearranjando os termos:
Cancelando termos opostos:
Agora lidando com :
Fatorando o termo e rearranjando os termos:
Cancelando termos opostos:
Assim, a equação 1:
Se torna:
Simplificando, temos:
Que é a equação 3.
Passo 3
Agora usando a aproximação pelo polinômio de Taylor de grau 3 para . Vamos calcular essa aproximação.
Calculando as derivadas de até a ordem 3:
Função original:
Primeira derivada:
Segunda derivada:
Terceira derivada:
Vamos centrar nosso polinômio em . Assim, substituindo:
Função original:
Primeira derivada:
Segunda derivada:
Terceira derivada:
E o polinômio de Taylor fica:
Como o segundo e o quarto, termo zeram, ficamos com:
Passo 4
Substituindo isso que acabamos de achar na equação 2:
Ou seja, fazendo :
Fazendo a mesma substituição para :
Temos:
Como já da pra ver que isso vai fizar uma coisa gigaaaante, vamos desenvolver primeiro só pro :
Abrindo o termo e fazendo as multiplicações:
Aplicando a propriedade distributiva da multiplicação:
Cancelando termos opostos e simplificando:
E como a gente vai ter que usar a série bonimial pra isso aí, vamos reescrever isso dai na forma:
Então colocando em evidência:
Fatorando
Tirando a raiz quadrada, podemos tirar para fora:
Fazendo exatamente a mesma coisa para a gente chega no seguinte resultado:
Passo 5
Da equação 1, temos
Que pode ser reescrito como sendo:
Vamos reescrever e . Temos que:
O próximo passo, agora, será calcular e expandindo em termos binomiais:
Passo 6
Lembrando que a série binomial é:
Queremos apenas os dois primeiros termos (de acordo com o enunciado), de forma que:
Usando os dois primeiros termos na série binomial para aproximar e :
Aqui, temos e . Logo,
Da mesma forma, temos que:
Finalmente, podemos continuar. Temos que:
Agora já temos e . Segue que:
- Cálculo de
- Cálculo de :
- Cálculo de :
- Cálculo de
Juntando tudo isso temos que:
Agora, devemos juntar os termos que são mais ou menos semelhantes:
Observe que:
Ou seja,
Colocando em evidência,
Da mesma forma, temos que:
Ou seja,
Ufa... Mas ainda não acabou!
Passo 7
Queremos chegar na equação 4
E até agora estamos em
Quer dizer, tá quaaaaaaase lá!
Comparando as duas equações, significa que ta faltando a gente provar que
E, para isso, vamos olhar para essa figura, que mostra uma onda de uma fonte pontual encontrando uma interface esférica de raio centrada em :
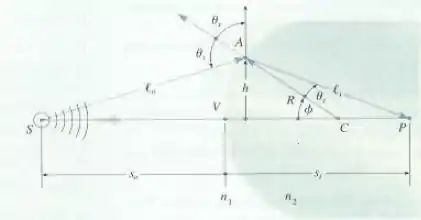
Nela, podemos ver que
Logo
E, como o enunciado sugere, , então
Assim, nossa equação fica exatamente igual a equação 4.
Resposta
Partes a) e b) demonstradas.