Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.5 - Ex. 3
Defina bola aberta de centro em e raio no . Interprete geometricamente
Passo 1
Já que vamos fazer a definição para , vamos no basear na definição feita para o .
Lá diz que a definição de uma bola aberta de centro em e raio ou seja
E, pela interpretação analítica, o que caracteriza a bola aberta é que a distância entre o ponto dado e centro seja menor que o raio.
Sendo assim, vamos definir nossa bola como sendo
Onde e
Passo 2
Vamos entender o que o conjunto nos diz geometricamente, tá? Para isso, vamos reescrevê-lo usando a definição de distância em .
Ou seja,
Considerando um ponto na bola aberta, satisfaz
Elevando ao quadrado,
Que se a gente reparar direitinho é a equação de uma esfera transladada, só muda que não bate a igualdade, o que significa dizer que estamos considerando apenas a parte de dentro da esfera. Em outras palavras, temos uma esfera maciça sem a casca.
Passo 3
Vamos entender a interpretação geométrica, beleza?
Se a equação lá de cima poderia ser desenhada assim
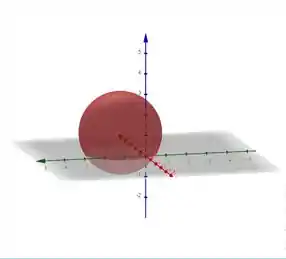
Mas nós só consideraríamos a parte de dentro da esfera, não a casca. Belezau?
Resposta
Podemos definir como o conjunto
Onde e E interpretar geometricamente como uma esfera maciça sem a casca.