Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 59

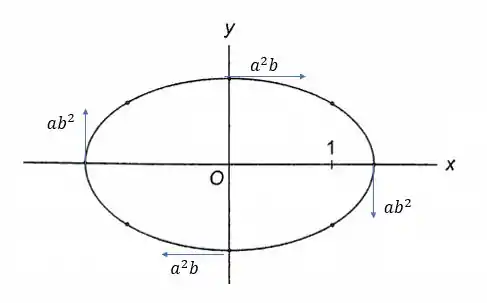
A elipse da Figura 22 - 23 tem equação x 2 p + y 2 q = 1

( a ) Desenhe, para cada ponto indicado, o representante do versor de t → = ( p k , - q h   ) , que tem origem nesse ponto

( b ) Uma partícula desloca-se ao longo da elipse e sua velocidade em cada ponto P = ( h , k ) é o vetor tangente t → = ( p k , - q h ) nesse ponto. Calcule, em função dos parâmetros geométricos a , b , as velocidades escalares máxima e mínima da partícula e os pontos em que ela atinge essas velocidades.

Passo 1

Vamos primeiro desenhar os versores e depois explicar cada um deles:

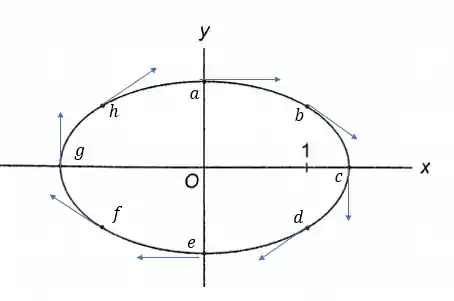
Onde cada versor tem equação igual a t → = ( p k , - q h ) , onde o ponto de interesse está em P = ( h , k ) ,o contrário saca?

Em a teremos h = 0 e k > 0 logo o versor aponta inteiramente para a direita ou seja t → = ( p k , 0 ) .

Em b teremos h > 0 e k > 0 logo o versor aponta para a direita e para baixo ou seja t → = ( p k , - q h ) , pois p k aponta para a direita e - q h aponta para baixo.

Em c teremos k = 0 logo o versor aponta inteiramente para a baixo ou seja t → = ( 0 , - q h ) .

Em d teremos h > 0 , k < 0 logo o versor aponta para a esquerda e para baixo ou seja t → = ( - p k , - q h ) .

Em e teremos h = 0 e k < 0 logo o versor aponta inteiramente para a esquerda ou seja t → = ( - p k , 0 ) .

Em f teremos h < 0 e k < 0 logo o versor aponta para cima e para a esquerda ou seja t → = ( - p k , q h ) .

Em g teremos h < 0 e k = 0 logo o versor aponta inteiramente para cima ou seja t → = ( 0 , q h ) .

Em h teremos h < 0 e k > 0 logo o versor aponta para cima e para a direita ou seja t → = ( p k , q h ) .

Passo 2

Considerando a o eixo maior e b 0 eixo menor então temos que para p = a 2 e q = b 2 teremos um vetor de velocidade escalar (ou tangencial) igual a:

  t → = ( a 2 k , - b 2 h )

Logo nas extremidades do eixo maior (eixo horizontal, portanto P = ( ± a , 0 ) ) teremos:

  t → = a 2 ⋅ 0 , - b 2 ⋅ ± a → t → = ± a b 2

E nos pontos do eixo menor (eixo vertical) teremos P = ( 0 , ± b ) :

  t → = a 2 ⋅ ± b , - b 2 ⋅ 0 → t → = ± a 2 b

Qualquer ponto entre esses dois extremos nos dará velocidades escalares intermediárias a essas duas.

E como a > b então velocidade escalar máxima é a 2 b e a mínima a b 2

Resposta

a )   E x p l i c a ç ã o   d o   p a s s o   1

b )   m á x i m a : a 2 b   n a s   e x t r e m i d a d e s   d o   e i x o   m e n o r ;

m í n i m a : a b 2   n a s   e x t r e m i d a d e s   d o   e i x o   m a i o r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam: e a excentricidade de uma curva C (elipse ou hipérbole), F um foco, r a diretriz associada a F , e m a distância de F a r . Exprima a , b e c em função de e , m nos casos: C é uma elipse; C é u
Sejam e a excentricidade da elipse E : x 2 / p + y 2 / q = 1 e F um de seus focos. Prove que, se P é um ponto qualquer de E , não pertencente ao eixo maior, e N é o ponto de interseção da reta normal
Verifique se vale uma propriedade semelhante à propriedade de reflexão: Quando se substituem, no seu enunciado, F 1 e F 2 por A 1 e A 2 ; Quando se substituem F 1 e F 2 por B 1 e B 2
O mecanismo da Figura 22-27 (b), conhecido como compasso elíptico, é formado por uma haste rígida, de comprimento m , cujas extremidades A e B são articuladas a blocos obrigados a movimentar-se nas re
Deduza as equações da elipse e da hipérbole que foram citadas no texto.