Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 53
Prove que:
Se é um ponto interior a elipse , então qualquer reta que contém é secante a
se é uma reta disjunta de , todos os pontos de são exteriores a (por essa razão, retas disjuntas de são também chamados exteriores a ).
Passo 1
Vamos imaginar um ponto e se ele está dentro da elipse é por que temos uma equação igual a:
E que nos darão equações iguais a:
E um valor de igual a:
E o valor de delta para essa equação nos dará:
Uma forma simplificada dessa equação será:
Da página 321 da terceira edição.
E a condição para essa reta ser uma secante é termos valores de , portanto acabaremos com:
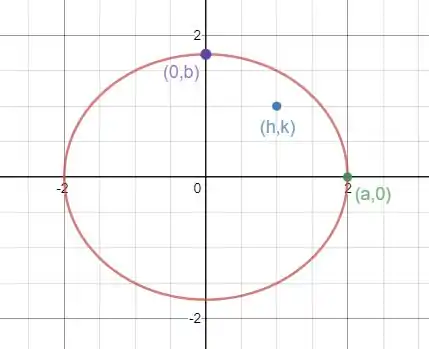
Uma vez que e (por P estar dentro da elipse como pode se ver na figura abaixo), portanto sempre teremos , nos dando somente retas secantes para um ponto dentro da elipse.
Passo 2
Para:
E para ser uma reta disjunta (externa) basta fazermos para o discriminante da elipse e para ser disjunta de nenhum ponto da reta deve pertencer a elipse. Para isso ser válido nós deveremos ter:
Ou seja:
Então para termos um resultado negativo basta termos as duas condições que são:
E por ter termos ao quadrado então:
Então somente teremos pontos externos a elipse como retas adjuntas, para fazer com que a equação acima dê certo. Lembrando que é um ponto exterior a elipse e que essa condição se mantém para qualquer ponto da reta disjunta.