Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.1 - Ex. 134

Definição recursiva de π 2 . Se você começar com x 1 = 1 e definir os termos subsequentes de { x n } pela regra x n   =   x n - 1   + cos ⁡ x n - 1 , você gerará uma sequência que converge rapidamente para π 2 . (a) Tente isso. (b) Use a figura a seguir para explicar por que a convergência é tão rápida.

Passo 1

Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?

(a)

Para fins de aproximação, temos que π 2 ≈ 1.5708 . Usando a formula recursiva, temos que:

x 1 = 1

x 2 = 1 + c o s ⁡ ( 1 ) = 1.540302306

x 3 = 1.540302306 + c o s ⁡ ( 1.540302306 ) = 1.570791601

x 4 = 1.570791601 + c o s ⁡ ( 1.570791601 ) = 1.570796327

x 5 = 1.570796327 + c o s ⁡ ( 1.570796327 ) = 1.57079632 7

​

Como você pode ver, a convergência da sequência para π 2 é realmente muito rápida.

Passo 2

(b)

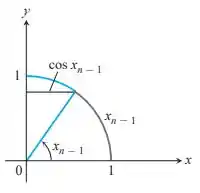
Da figura geométrica abaixo, sabemos que o arco azul representa o comprimento do arco de x n - 1 ​ e o arco vermelho representa o comprimento do arco de π 2 - x n - 1

Da mesma forma, o segmento de linha azul representa cos ⁡ x n - 1 . Como o comprimento do arco π 2 - x n - 1 ​ aproxima-se de π 2 , o segmento de reta cos ⁡ x n - 1 e o comprimento do arco π 2 - x n - 1 ​

aproxima-se de 0. Essa convergência é muito rápida porque cos ⁡ x n - 1 já é grande em relação a x 1 = 1 para começar, então depois de alguns passos, a sequência converge.

Espero ter ajudado! Abraços e até a próxima!

Resposta

Veja a demonstração acima.

Exercícios de Livros Relacionados

Nos Exercícios 13-26, encontre uma fórmula para o n -ésimo termo da sequência.A sequência 1 ,- 1 ,1 ,- 1 ,1 , … (Números 1 com os sinais alterados.)
Nos Exercícios 13-26, encontre uma fórmula para o n -ésimo termo da sequência. 1 9 , 2 12 ,2 2 15 ,2 3 18 , 2 4 21 ,… (Potências de 2 divididas por múltiplos de 3.)
Nos Exercícios 13-26, encontre uma fórmula para o n -ésimo termo da sequência. - 3 2 ,- 1 6 , 1 12 , 3 20 , 5 30 ,… (Inteiros diferindo por 2 divididos por produtos de inteiros consecutivos.)
Nos Exercícios 13-26, encontre uma fórmula para o n -ésimo termo da sequência.A sequência 0 ,3 ,8 ,15 ,24 ,. . . (Quadrados dos inteiros positivos menos 1.)
Nos Exercícios 13-26, encontre uma fórmula para o n -ésimo termo da sequência. 5 1 , 8 2 , 11 6 , 14 24 , 17 120 , … (Inteiros diferindo por 3 divididos por fatoriais.)