Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 39
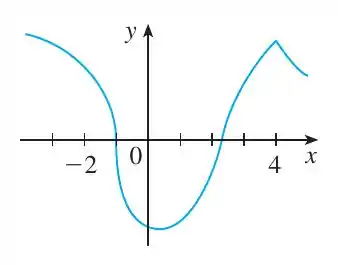
O gráfico de f é dado. Indique os números nos quais f não é diferenciável.
Passo 1
Beleza, meu nobre amigo?! Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui iremos analisar onde a função não pode ser diferenciada, isso é, onde sua derivada não existe.
Em geral, se o gráfico de uma função f tiver uma “quina” ou uma “dobra”, então o gráfico de f não terá tangente nesse ponto e f não será diferenciável ali.
O Teorema 4 nos dá outra forma de uma função deixar de ter uma derivada. Ele afirma que
se não for contínua em a, então f não é diferenciável em a. Então, em qualquer descontinui-
dade (por exemplo, uma descontinuidade de salto) f deixa de ser diferenciável.
Uma terceira possibilidade surge quando a curva tem uma reta tangente vertical quando a; isto é, f é contínua em a e
Passo 2
Beleza, agora vamos interpretar o nosso gráfico. O gráfico não é diferençável em porque a tangente é vertical.
O gráfico não é diferençável em porque há um canto/aresta.
Resposta
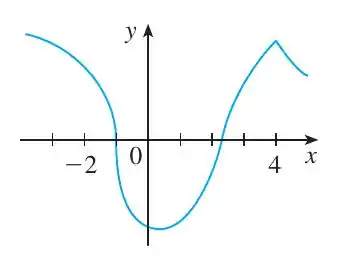
O gráfico não é diferençável em porque a tangente é vertical.
O gráfico não é diferençável em porque há um canto/aresta.