Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 15
Demonstre cada afirmação usando a definição , de limite e ilustre com um diagrama como o da Figura 9.
15.
Passo 1
Fala aí, galerinha! 👀
Nesse problema temos que demonstrar que usando as definições e .
Lembra como fazemos isso? 😉
A definição precisa de limite nos diz que seja uma função definida em algum intervalo aberto que contenha um número , temos
Se para todo houver um número de modo que
Então, temos
Bora começar! 😁
Passo 2
Dado que , nós precisamos achar , tal que se:
Então temos que:
Vamos agora simplificar isso:
O que nos mostra que se:
Então:
Tranquilo até aqui? 👀
Passo 3
Isso nos dá que se nós escolhemos , e substituirmos seu valor, temos que
Portanto, temos o limite
pelo limite da definição.
Passo 4
Aqui temos o diagrama:
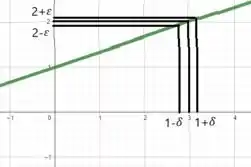
E aí! o que achou? Responde Aí! 😬
Resposta
Exercícios de Livros Relacionados
Use a Definição 5.4.3 tomando como a extremidade esquerda de cada subintervalo para encontrar a área sob a curva y = f ( x ) acima do intervalo especificado. f x = x 2 ; 1,4
Use a Definição 5.4.3 tomando como x k * como o ponto médio de cada subintervalo para encontrar a área sob a curva y = f ( x ) acima do intervalo especificado. f x = 6 - x ;1,5
Divida o intervalo em n = 4 subintervalos de igual tamanho, e netão calcule ∑ k = 1 4 f x k *∇ x Tomando x k * com (a) extremidade esquerda de cada subintervalo, (b) o ponto médio de cada subintervalo
Divida o intervalo em n = 4 subintervalos de igual tamanho, e netão calcule ∑ k = 1 4 f x k *∇ x Tomando x k * com (a) extremidade esquerda de cada subintervalo, (b) o ponto médio de cada subintervalo
Divida o intervalo em n = 4 subintervalos de igual tamanho, e netão calcule ∑ k = 1 4 f x k *∇ x Tomando x k * com (a) extremidade esquerda de cada subintervalo, (b) o ponto médio de cada subintervalo