Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.1 - Ex. 34
Use um gráfico para encontrar as coordenadas aproximadas de x dos pontos de intersecção das curvas dadas. Encontre a área de uma região limitada pelas curvas.
Passo 1
De inicio, precisamos do gráfico, então plotamos:
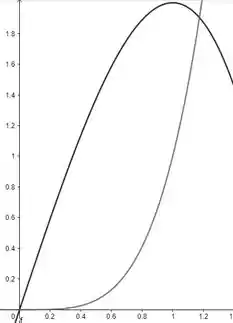
Pelo gráfico, nós podemos perceber que ele intercepta o eixo nos pontos onde e , com em . Certinho?? , esse valor nos ajuda a saber os intervalos da nossa integral!!
Então a área da região limitada pela curva é dada por:
Agora é só resolver!!!
Resolvendo a nossa integral, temos
Prontinho!!
Resposta
Exercícios de Livros Relacionados
Esboce a região delimitada pelas curvas indicadas e encontre sua área. x = y 4 , y = 2 - x , y = 0
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = cos π x , y = 4 x 2 - 1
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área correta até a quinta casa decimal. y = e 1 - x 2 ,y = x 4
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área correta até a quinta casa decimal. y = tan 2 x ,y = x
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = cos x , y = sin 2 x , x = 0 ,x = π 2