Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 40
Demonstre que
Passo 1
Faaaala galerinhaaa, como vocês estão? Animadíssimos? Então booooraa!!
Seguinte... queremos demonstrar a seguinte igualdade:
Parece complicado?
Como o primeiro passo de todo limite é substituir e ver no que dá, temos:
Mas perai gente, existe? A função é oscilatória!
Então não tem como tender pra nada no infinito, nem mesmo algum dos infinitos.
Como esse limite não dá pra calcular, vamos ter que tentar alguma outra estratégia!
Nesse caso, como temos um seno que multiplica outra função, podemos aplicar o teorema do confronto.
O teorema do confronto diz que:
Sejam , funções reais definidas no dominio e seja a um ponto dentro desse dominio, se:
E
Então
Bora pensar!
Passo 2
Vamos começar analisando a função seno, ok? E sabemos que ela é limitada superiormente por , e inferiormente, , não é?
Importantíssimo: Isso independe da expressão dentro do seno!
Em inequação:
Até aqui tudo muito tranquilo, mas não é isso que queremos, nós precisamos saber os intervalos de .
Então o que fazemos? Pra começar, olha o macete, imagina que eu tenha:
Ok, mas e dai? Bem, se esses números forem expoentes de , por exemplo, vai ser válido também:
Portanto podemos fazer a mesma coisa, só que aplicando o exponencial dessa vez, ficando assim com a cara da nossa função!!! Vamos ter
E multiplicando dos dois lados por
Tranquilo até aqui?
Passo 3
Tá na mão! Nossa função apareceu! Podemos, pelo Teorema do Confronto, afirmar que:
Vamos analisar os limites inferior e superior então
Ou seja, quanto mais próximo o está de zero, mais próximo está de zero e, consequentemente, mais próximo tanto a função quanto a função estarão de zero!
Completamos nossa inequação então da seguinte forma:
Oras, se um número está entre e , então ele é igual a zero!
E comprovamos o que queríamos, não é? Feshow
Passo 4
Só pra gente conseguir ver graficamente, olha como fica o teorema do confronto pras três funções da inequação:
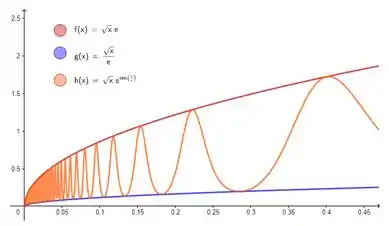
E fim! O que achou? Responde Aí!
Resposta
Por Teorema do Confronto, é possível provar que