Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.3 - Ex. 42
Encontre, quando existir, o limite. Caso não exista, explique por quê.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o limite da função quando tende a .
Repare que se a gente substituir na função, teríamos uma indeterminação do tipo . Então, vamos ter que achar uma forma de fugir dessa indeterminação antes de aplicar o limite. Pra isso, vamos começar analisando nossa função.
Observe que nós temos uma função modular no denominador, que pode ser definida por partes na forma:
Isso significa que pode tender a por valores maiores do que , ou seja, pela direita, ou pode tender por valores menores que , ou seja, pela esquerda.
Dessa forma, nós vamos precisar calcular os limites laterais dessa função usando as duas condições da sua definição:
Se esses limites existirem e forem iguais, encontraremos o limite de pra quando tende a () e teremos nossa resposta. Então, vamos tentar simplificar a função em ambos os casos e aplicar o valor do limite.
Vamos lá!
Passo 2
Vamos começar calculando o limite lateral pela direita, fazendo tender a por valores maiores que :
Como a gente viu no passo , se a gente só substituir teremos uma indeterminação. Então, vamos tentar simplificar essa fração antes de aplicar o limite. Vamos fazer isso colocando em evidência no numerador:
Agora repare que nós temos no numerador e no denominador, então podemos simplificar os dois termos e ficamos com:
Agora ficou moleza, né? É só substituir o valor do limite e teremos:
Passo 3
Já calculamos o limite pela direita, agora vamos calcular pela esquerda e ver se o resultado bate.
Nós vimos que quando tende a por valores menores que , temos o limite lateral:
Vamos colocar em evidência novamente e simplificar, como fizemos no passo anterior:
E aí é só aplicar o limite no lugar do :
Opa! Os limites laterais deram valores diferentes, olha só:
Isso significa que o nosso limite de quando não existe, ou seja:
Só por curiosidade, dá uma olhadinha no gráfico dessa função:
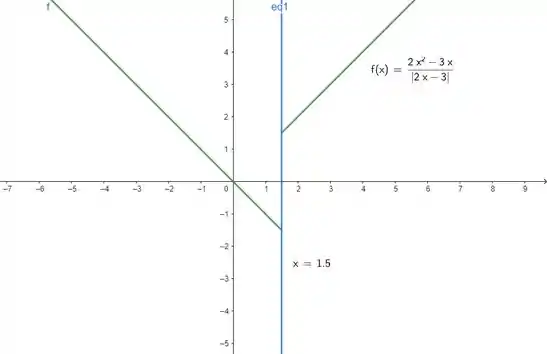
Em verde nós temos a função e em azul a reta . Observe que a nossa função tem uma quebra nesse ponto e que caminhando pela direita nós nos aproximamos de um valor e pela direita nos aproximamos de outro. Por isso, o limite não existe.
Valeu, galera! Até a próxima! 😉