Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 2
Demonstre que, entre todos os retângulos com perímetro de 8 m, o de maior área é um quadrado.
Passo 1
O Perímetro e a área de um retângulo são dadas por:
Passo 2
Primeiro iremos transformar nossas equações de duas variáveis em uma equação de uma variável. Como temos que P= 8 , podemos pegar a expressão:
Substituindo isso na equação da área temos que:
Passo 3
Para achar o maior área possível, podemos derivar a expressão, e igualar a 0. Assim a derivada ficará:
Passo 4
Substituindo no perímetro e na expressão da área, temos que:
Logo
,
A resposta pode ser vista no gráfico abaixo:
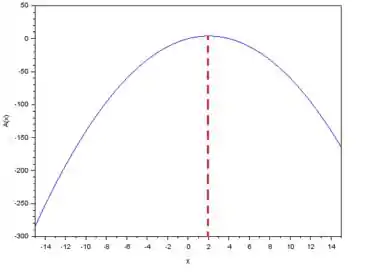
Reparem na concavidade para baixo, o que indica que:
Resposta
Temos aqui um quadrado de lado 2.
Exercícios de Livros Relacionados
Suponha que a refinaria do Exercício 47 esteja localizada 1k m ao norte do rio. Onde P deveria estar situado?
Uma refinaria de petróleo está localizada na margem norte de um rio reto que tem 2k m de largura. Um oleoduto deve ser construído da refinaria até um tanque de armazenamento localizado na margem sul d
Mostre que, de todos os triângulos isósceles com um dado perímetro, aquele que tem a maior área é o equilátero.
Os ornitologistas determinaram que algumas espécies de pássaros tendem a evitar voos sobre largas extensões de água durante o dia. Acredita-se que é necessária mais energia para voar sobre a água que
A seção transversal de uma tina tem a forma de um triangulo isósceles invertido. Se o comprimento dos lados iguais for de 15 cm , ache a medida do ângulo do vértice que dará capacidade máxima à tina.