Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 9
Determine o limite
Passo 1
Antes de calcularmos o limite, vamos analisar a função que está em jogo, certo ?
Temos a função .
Se olharmos para o numerador da função, temos uma variação da função seno. Vamos analisar o gráfico dessa função, beleza?
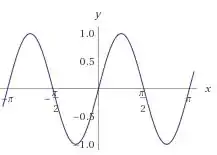
Olhando bem rapidinho, dá pra ver que assim como o seno, ela varia entre e . Isso significa dizer que
Mais ainda, significa dizer que
Se você parar pra fuçar a memória, vai lembrar de uma parada em que calculamos o limite entre desigualdades... lembrou? O nome dessa bagaça é Teorema do confronto, ou teorema do sanduíche, que é onde uma função fica apertada por outras duas como a carne de hamburguer fica entre o pão e ai é só aplicar o limite em todas as desigualdades, né? .
Mas e aí? Cabou? Já podemos aplicar o limite ?
Não! A função que temos que calcular o limite é , então falta uma parte, beleza ?
A gente pode fazer ela aparecer, é só multiplicar o que a gente precisa aqui ó:
Passo 2
Você já sacou que tem que multiplicar por todo mundo ali em cima e aplicar o limite, né?
Mas só posso fazer isso tranquilamente porque como temos que então e quando multiplicar em
A desigualdade fica intacta, ou seja,
Então, vamos lá, podemos passar o limite agora e nossa conta fica assim:
Passo 3
Cabe a nós, meros mortais sabermos que que acontece com esses caras aqui:
e
Tá ligado que esse limites são zero ne? Sabe, o motivo?
Vou tentar contextualizar rapidinho:
Imagine que você tem R$10,00 para dividir para nós dxs, beleza ? Então, a quantidade que vamos receber seria R$5,00 Mas e se agora você tiver que dividir para cem pessoas, o valor vai ser bem menor, não é ? Mas e se for para mil pessoas? Menor ainda, concorda comigo, migxs? Então, o valor recebido por cada um de nós é cada vez menor à medida que aumentamos a quantidade de pessoas que temos que dividir o money, ou seja, estamos ficando com quase nada, né?!! O valor a receber por nós tende a zero.
Tá, se olharmos para esse R$10,00 como nosso e fazermos tender a infinito é como se estivessemos dividindo o 5 por valores cada vez maiores, consequentemente
E como
Então, finalmente podemos concluir alguma coisa sobre o limite nesse primeiro caso... Já que
E
Pelo teorema do Confronto/ Sanduiche,