Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.2 - Ex. 7

Derive a função:

g ( x ) = (3 x - 1)/(2 x + 1)

Passo 1

E aí, pessoal! 😎

Bom, galera... precisamos derivar a função.

g ( x ) = (3 x - 1)/(2 x + 1)

Mas neste caso a função é composta por uma divisão, então o que fazemos?

Usamos a Regra do Quociente!

Então:

y ' = (( 2 x + 1 ) . (d)/(d x) (3 x - 1) - ( 3 x - 1 ) . (d)/(d x) (2 x + 1))/(( 2 x + 1 ) ²)

Veja só! 😐

Passo 2

Agora vamos lembrar a Derivada da Soma e da Subtração:

y ' = ((2 x + 1) . [(d)/(d x) 3 x - (d)/(d x) 1] - (3 x - 1) . [(d)/(d x) 2 x + (d)/(d x) 1])/(( 2 x + 1 ) ²)

E qual é a derivada de uma constante?

Vamos relembrar:

y ' = ((2 x + 1) . [(d)/(d x) 3 x - 0] - (3 x - 1) . [(d)/(d x) 2 x + 0])/(( 2 x + 1 ) ²)

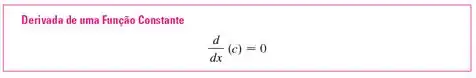
A constante pode sair de dentro da derivada. Se lembram?

y ' = ((2 x + 1) . [3 (d)/(d x) x] - (3 x - 1) . [2 (d)/(d x) x])/(( 2 x + 1 ) ²)

Para finalizar vamos usar a Regra da Potência:

y ' = ((2 x + 1) . [3.1] - (3 x - 1) . [2.1])/(( 2 x + 1 ) ²)

Abrindo a equação:

y^' = (6 x + 3 - (6 x - 2))/((2 x + 1)^2) = (6 x + 3 - 6 x + 2)/((2 x + 1)^2)

Sendo assim:

y^' = (5)/((2 x + 1)^2)

Bacana, não é? Responde Aí! 😊

Resposta

y^' = (5)/((2 x + 1)^2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 23-26, determine d r // d theta .23. r= 4 - theta^2 sen theta
Nos Exercícios 1-18, determine d y // d x .18. g ( x ) = (2 - x) tg^2 x
Nos Exercícios 23-26, determine d r // d theta .24. r= theta sen theta + cos theta
Determine a derivada da função.r = (e^s)/(s)
Determine as derivadas das funções nos Exercícios 17-40. w = 1 z 1,4 + π z