Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 7.2 - Ex. 34
Desconto contínuo no preço. Para incentivar os compradores a fazer pedidos de 100 unidades, o departamento de vendas de sua empresa aplica um desconto continuo que toma o
preço por unidade uma função do número de unidades pedidas. O desconto diminui o preço a uma taxa de por unidade pedida. O preço unitário para um pedido de 100
unidades é.
a. Determine p(x) resolvendo o seguinte problema de valor
inicial:
Equação diferencial:
Condição inicial:
b. Determine os preços unitários para um pedido de unidades e para um pedido de 90 unidades.
c. O departa1nento de vendas pediu para que você descubra se o desconto oferecido é tal que a receita da empresa, realmente será menor para um pedido de unidades do que para um pedido de unidades. Tranquilize-os, mostrando quer tem seu valor máximo em.
d. Faça o gráfico da função receita para.
Passo 1
Inicialmente para resolver a EDO, reorganizaremos os termos, isso significa que de um lado fica todo mundo que depende de e do outro todo mundo que depende de
Integrando ambos os lados em relação a suas respectivas variáveis, teremos que
Portanto, a solução da EDO é da forma,
Assim,
Onde,
Como desejamos encontrar apenas , então
Considerando teremos,
Como teremos,
Sendo assim,
Passo 2
Perceba que para teremos
Da mesma forma, para teremos
Passo 3
Sabemos que
Desejamos saber se será de fato o menor, para utilizaremos a derivada, ou seja,
Por outro lado,
Assim,
Vamos verificar agora se , de fato é um mínimo, ou seja,
Perceba que para , . Por outro lado, quando , . Sendo assim, em assume um máximo.
Passo 4
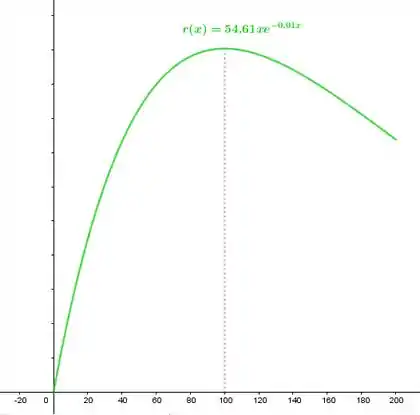
Utilizando os dados que temos a respeito da derivada, obteremos o gráfico da forma:
Resposta
Item a.
Item b. e
Item c. assume um máximo em
Item d.
