Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 19
Descreva o movimento de uma partícula com posição (x, y) quando t varia no intervalo dado
Passo 1
Vamos descobrir como lemos funções no formato paramétrico. Primeiro, você pode sempre voltar para o formato cartesiano, e sinta-se à vontade a seguir pelo caminho que você achar mais confortável. Nossas equações são:
Vamos lá, nosso x e y são funções trigonométricas. Isso significa que nosso gráfico é alguma espécie de cônica. Podemos ver parábolas, círculos, hipérboles ou elipses. Tudo vai depender de como nossa função está parametrizada. Pegando por exemplo o
Essa função quer dizer que o centro da nossa cônica é em , e o multiplicando o cosseno é que do centro da cônica até a extremidade do eixo x é 2. Podemos pensar que o raio nesse eixo é 2.
Em y, temos que o centro da cônica é , e o raio nesse eixo também é 2. Isso quer dizer que estamos trabalhando com um círculo. Sempre que os raios forem iguais então temos um círculo, caso contrário será uma elipse. Então beleza, sabemos que nossa função é um círculo, de raio 2 e centro em (5,3).
Passo 2
Uma dica importante. Isso você vai pegar a pratica com o tempo, mas posso te dar esse spoiler. Rsrs. Sempre que estivermos com
Nossa função é circular e horaria. E além disso começamos a desenhar com em . Agora quando temos:
Nossa função é circular, anti-horária. E começamos a desenha com em . Então beleza, e como fica então nosso gráfico?
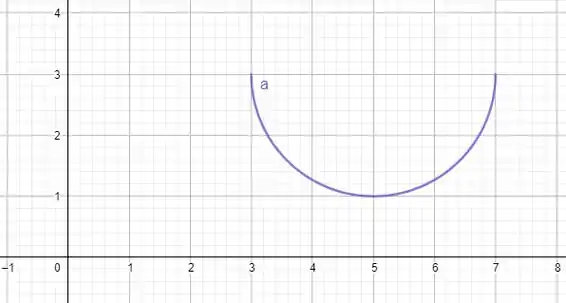
Como nosso parâmetro está limitado em então teremos apenas umas partezinha do nosso círculo. Tudo certo? Terminamos por aqui, te vejo na próxima resolução : )
Resposta
Ei, a resposta está no passo a passo :)