Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 2

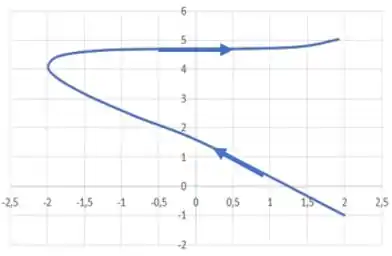
Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando aumenta

Passo 1

Eaee, belezinha?? Bom... O enunciado nos deu as seguintes equações paramétricas para o intervalo :

Queremos esboçar a curva de utilizando pontos. Em seguida, vamos indicar com uma seta a direção na qual a curva é traçada quando aumenta.

Para esboçar a curva, precisaremos aplicar alguns valores em e marcar os pontos no plano cartesiano para, em seguida, traçarmos o gráfico.

Agora bora lá!! 😉

Passo 2

Atribuindo alguns valores para dentro do intervalo dado e analisando seus valores em e , obtemos:

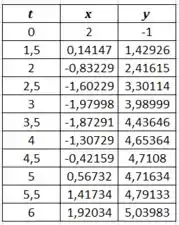
Agora vamos marcar os pontos em um gráfico:

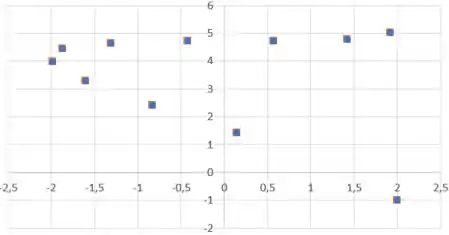
Se ligarmos os pontos, teremos um gráfico assim:

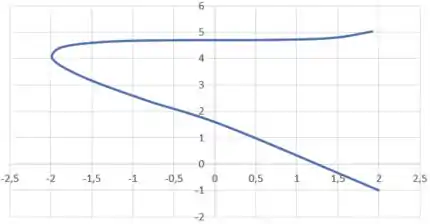
Passo 3

Agora, analisando cada ponto do gráfico para cada valor de temos que, quando aumentamos o valor de os pontor aparecem nessa direção:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = 1 + 2 sen ⁡ ( θ / 2 ) (nefroide de Freeth)

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = 2 - 5 sen ⁡ ( θ / 6 )

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = e sen ⁡ θ - 2 cos ⁡ ( 4 θ ) (curva em borboleta)

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = sen 2 ⁡ ( 4 θ ) + cos ⁡ ( 4 θ )

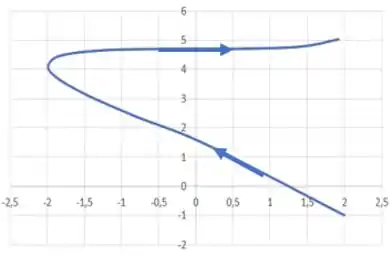
Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = 1 - 0,8 sen 2 ⁡ θ (hipopédia)