Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.6 - Ex. 32
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.
Passo 1
E aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é descrever como a função muda então varia.
Tem ideia de como fazemos isso?
A questão ainda nos deu uma dica bacana... vamos verificar como os pontos extremos e os pontos de inflexão variam a medida que varia.
Para isso vamos calcular e e analisar como a variação de impacta nessas funções.
Bora começar!
Passo 2
Note que é uma função par, pois todos as aparições de está elevado ao quadrado, então .
Além disso: para qualquer valor de , então é uma assíntota horizontal.
Vamos começar calculando as derivadas pela regra do quociente...
Aplicando a regra da potência:
Tranquilo até aqui?
Passo 3
Agora vamos calcular a derivada de segunda ordem:
Pra isso vamos aplicar a regra do quociente de novo.
Aplicando as regras da potência e da cadeia, vamos obter:
Bacana, não é?
Passo 4
Para o primeiro o caso vamos analisar a derivada de para :
O denominador de está elevado ao quadrado, então ele é sempre positivo. Além disso temos dois termos elevados ao quadrado que estão somando, então ele nunca vai ser igual a zero. Temos então:
Para todo , então tem domínio nos reais e .
Se , , então o único ponto crítico é , um máximo.
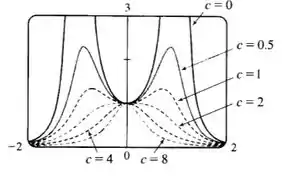
Colocando no gráfico de alguns exemplos para temos dois pontos de inflexão que se aproximam do eixo com :
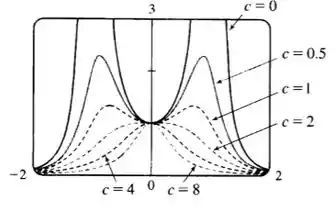
Tranquilo até aqui?
Passo 5
Em e são valores transitórios de em que as formas das curvas mudam. Para , há três pontos críticos: , um valor mínimo, e , ambos valores máximos.
Conforme decresce de a , o valor máximo fica cada vez maior, e os valores de em que eles ocorrem vão de a .
O gráfico mostra que há quatro pontos de inflexão para , e eles ficam cada vez mais longe da origem, verticalmente e horizontalmente, quando
Para , a função é simplesmente uma assíntota do eixo , e das retas , se aproximando de dos dois lados. O intercepto é e é um ponto mínimo local. Não há pontos de inflexão.
Show?
Passo 6
Agora, se , podemos reescrever a função como
Assim, tem assíntotas verticais quando:
Ou então:
Está acompanhando? 👀
Passo 7
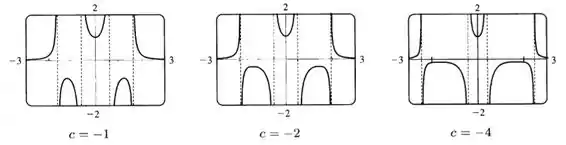
Conforme decresce, as duas assíntotas exteriores se movem para longe da origem enquanto as duas assíntotas interiores se movem para próximo dela. Nós podemos colocar no gráfico alguns exemplos para ver o comportamento do gráfico perto das assíntotas, e a natureza dos pontos críticos e
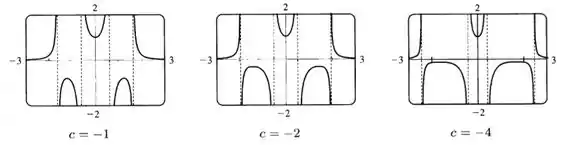
Nós vemos que há um valor mínimo local, , e há dois máximos locais, como antes. Conforme diminui, os valores de e que há máximos ficam maiores, e os valores máximos se aproximam cada vez mais de , apesar de eles serem sempre negativos.
É isso! O que achou? Responde Aí!
Resposta
