Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 5
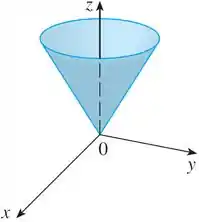
Descreva com palavras a superfície cuja equação é dada.
Passo 1
Fala, minha gente! Tudo tranquilo?
A questão quer que a gente descreva em palavras a superfície caracterizada por:
Bem, só de olhar nossa variável já entendemos que essa superfície se encontra em um sistema de coordenadas esféricas, onde os pontos são do tipo . Então, vamos entender como se dá a variação de cada variável e o que ela representa, assim a gente consegue visualizar nossa superfície.
Vamos lá!
Passo 2
Show de bola, galera! Pra resolver essa questão não tem mistério. Basta nos lembrarmos do conceito de coordenadas esféricas.....
A coordenada corresponde ao ângulo entre o segmento de reta que representa o raio da nossa esfera (por isso coordenadas esféricas, né) e o eixo . Esqueceu? Dá uma olhada na figura abaixo.
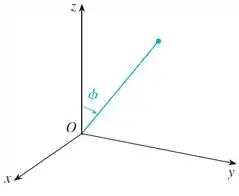
Como
e e podem assumir qualquer valor, é só olhar pra figura de cima e imaginar que o segmento se extende indefinidamente e que ele pode girar à vontade no plano .
Isso vai gerar um cone na metade superior do plano igual ao ilustrado na figura abaixo.
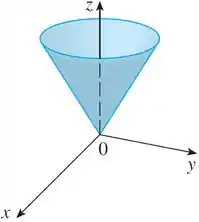
Resposta
Cone na metade superior do plano .
