Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.3 - Ex. 31

E aii, tudo certo?

Nessa questão, nós temos um conjunto:

E precisamos determinar se ele é aberto, conexo por caminhos, e simplesmente conexo.

Vamos ver um por um:

Para ser aberto, precisamos que pra todo ponto do conjunto exista uma bola aberta centrado nesse ponto que esteja totalmente contido em .

Com menos “matematiquês”, podemos dizer que um conjunto é aberto quando os pontos que limitam não fazem parte dele.

ser conexo por caminhos quer dizer que quaisquer dois pontos em podem ser ligados por uma curva contida no conjunto.

Na prática, isso quer dizer que a região de no é “uma só”, em vez de ser contida por mais de uma região separadas.

E para o caso de ser simplesmente conexo, qualquer curva simples fechada em vai contornar somente pontos que pertencem à região.

Traduzindo: não tem nenhum “buraco” na região.

Então vamos analisar cada um dos casos!

Vamos desenhar a região definida pelo conjunto

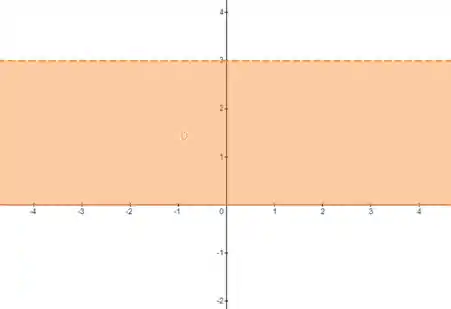
E agora vamos analisar cada uma das definições com base nesse desenho.

(a)

Percebe que pelo desenho, os limites da região são as retas e , que não fazem parte da região!

Portanto, é uma região aberta!

(b)

Ainda olhando pro desenho, temos que o conjunto define uma região única, toda contínua. Isso indica que é conexo por caminhos!

(c)

Por último, percebemos que não tem nenhum “buraco” no desenho de .

Ou seja, é um conjunto simplesmente conexo!