Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 70

Descreva as superfícies de nível da função.

f (x , y , z) = x^2 - y^2 - z^2

Passo 1

As curvas de nível da função são da forma x^2 - y^2 - z^2 = k . Temos 3 casos:

  • k = 0 : vamos ter x^2 = y^2 + z^2 , que é um cone com vértice em ( 0,0 , 0 ) .
  • k > 0 : x^2 - y^2 - z^2 = k , é uma família de hiperboloides de duas folhas.
  • k < 0 : x^2 - y^2 - z^2 = - k -> - x^2 + y^2 + z^2 = k , aqui vai ser uma família de hiperboloides de uma folha.

Passo 2

Vamos ver um exemplo de cada caso:

  • k = 0

  • k > 0

  • k < 0

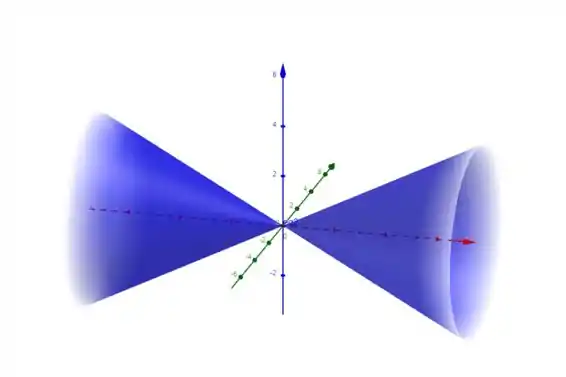
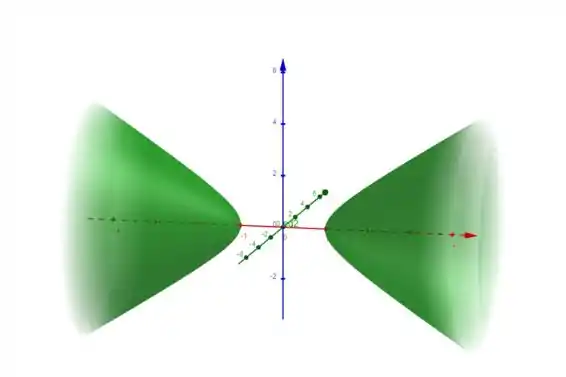
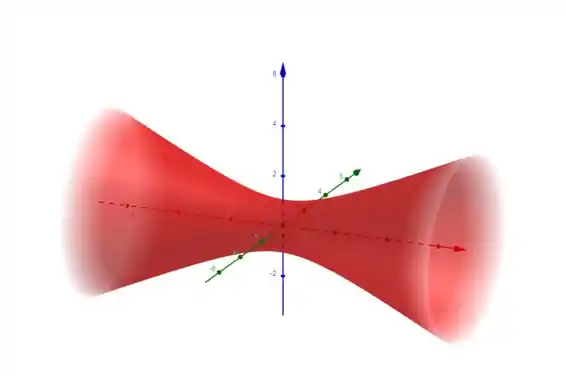
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 61-64, encontre uma equação para a superfície de nível da função que passa pelo ponto dado. f x ,y ,z = l n l nx 2 + y + z 2,- 1 ,2 ,1
Nos Exercícios 53-60, esboce uma superfície de nível típica para a função. f x ,y ,z = x 2 + y 2 + z 2
Nos Exercícios 65-68, encontre e esboce o domínio de f . Em seguida, encontre uma equação para a curva de nível ou superfície da função passando pelo ponto dado. f x ,y = ∫ x y d θ 1 - θ 2 ,0 ,1
Nos Exercícios 53-60, esboce uma superfície de nível típica para a função. f x ,y ,z = y 2 + z 2
Nos Exercícios 53-60, esboce uma superfície de nível típica para a função. f x ,y ,z = x + z