Nos Exercícios 53-60, esboce uma superfície de nível típica para a função.
Passo 1
Oi galerinha, tudo bem com vocês? Vamos fazer esse exercício juntos?! Então, vem comigo!
No plano, os pontos onde uma função de duas variáveis independentes tem um valor constante formam uma curva no domínio da função. No espaço, os pontos onde uma função de três variáveis independentes tem um valor constante formam uma superfície no domínio da função.
O conjunto de pontos no espaço onde uma função de três variáveis independentes tem um valor constante é chamado superfície de nível de .
No nosso exercício, temos a seguinte equação:
O valor de é a distância entre a origem e o ponto . As superfícies de níveis são , onde , é uma circunferência de raio centrada na origem. A superfície de nível consiste somente na origem.
Passo 2
No eixo e , temos uma circunferência, se considerarmos , temos uma circunferência de raio 1:
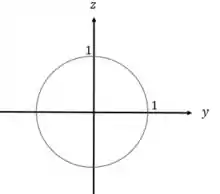
Para esboçar o gráfico no espaço, vamos utilizar o programa WolframAlpha, que nos fornece a seguinte curva:
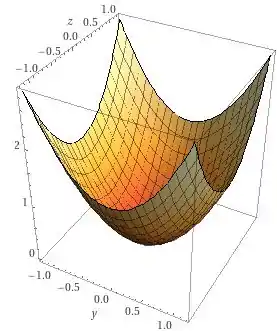
Até mais pessoal, espero vocês em mais exercícios!
Resposta
Resposta no Passo 2.