Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.5 - Ex. 82b
Dê uma descrição geométrica de cada família de planos:
Passo 1
Bom galera, vamos pensar um pouco quando :
Logo:
Passo 2
Então, a mudança de faz o plano rotacionar entorno da linha que achamos na função anterior, como por exemplo esse é o coeficiente angular da rotação do plano, que ficaria assim:
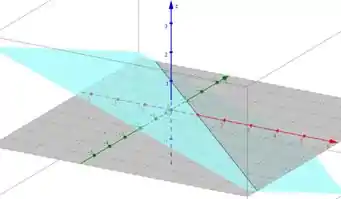
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Achar a distancia do ponto P à reta r nos casos P 1 , - 1 , 0 r : x = 2 - t y = 0 z = t
Achar a distancia do ponto P à reta r nos casos P 3,2 , 1 r : y = 2 x z = x + 3
Calcule a distância do ponto P à reta r .c) P = 1 , - 1,4 , r : x - 2 4 = y - 3 = 1 - z 2
Determine as coordenadas do simétrico ao ponto P = ( 2 , - 3 ) em relação a:a.Ao eixo OX;b.Ao eixo OY;c.À diagonal ∆ d.Ao ponto (-3,2).
Mostre que a equação da tangente à circunferência A x 2 + A y 2 + D x + E y + F = 0 no ponto x 1 , y 1éa x - x 1 + b y - y 1 = 0 é , onde a = x 1 + D 2 Aeb = x 2 + E 2 A