Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.6 - Ex. 12
Desenhe o conjunto A dado e calcule a área:
A é o conjunto de todos (x, y) tais que e .
Passo 1
Oi, pessoal! Nessa questão nós queremos a área entre . Então vamos começar esboçando os dois gráficos e , e verificando onde os dois se cruzam.
e
Como o problema diz que só está interessando na parte , a região que vamos integrar será:
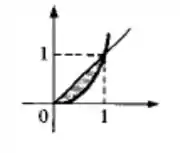
Agora que desenhamos a figura, vamos montar a integral!
Passo 2
Repara na figura que função maior é e a função menor é , e a nossa vai região vai de até , como isso temos que
Resposta
Exercícios de Livros Relacionados
Esboce a região delimitada pela curva fornecida e calcule sua área: y = 4 - x 2 , y = 0
Esboce a região delimitada pela curva fornecida e calcule sua área: y = x , y = 0 , x = 4
Esboce a região delimitada pela curva fornecida e calcule sua área: y = 2 x - x 2 , y = 0
Temos F x = ∫ 2 x e t 2 d t . Encontre uma equação da reta tangente para a curva y = F ( x ) no ponto da coordenada x = 2 .
7 – 18 Use a Parte 1 do Teorema Fundamental do Calculo para encontrar a derivada da função.8. g x = ∫ 1 x ln 1 + t 2 d t