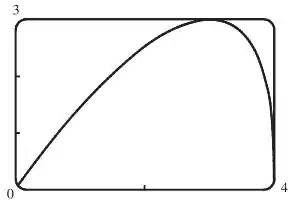
- Desenhe a curva
- Calcule os comprimentos das poligonais inscritas com e lados. (Divida o intervalo em subintervalos iguais.) Ilustre esboçando essas poligonais (como na Figura 6).
- Escreva uma integral para o comprimento da curva.
- Use sua calculadora para encontrar o comprimento da curva com precisão de quatro casas decimais. Compare com as aproximações na parte (b).
Passo 1
- Desenho:
- Esboço do desenho:
- Usando a fórmula de comprimento do arco com
- De acordo com uma calculadora, o comprimento da curva é . O valor real é maior do que qualquer uma das aproximações feitas na parte (b). Isso é sempre verdade, desde que qualquer aproximação pela reta esquerda entre dois pontos na curva é menor do que o comprimento da curva entre esses dois pontos.
Passo 2
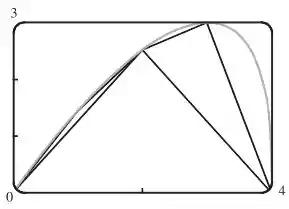
Digamos que O polígono de um lado é apenas o seguimento de reta unindo os pontos e , e seu comprimento é
O polígono de dois lados une os pontos , e . Seu comprimento é
Similarmente, o polígono inscrito com quatro lados une os pontos e , então seu comprimento é
Passo 3
o comprimento da curva é
Passo 4
Resposta
Ei, a resposta está no passo a passo :)