Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1h

Desenhe a curva dada (coordenadas polares ).

h ) rho^2 = (1)/(1 + sin^2 theta)

Passo 1

Para esse caso, podemos transformar em coordenadas cartesianas:

Quando fazemos:

rho^2 (1 + sin^2 theta) = 1 -> ( rho^2 + rho^2 sin^2 theta ) = 1

Sabemos que para transformar uma cordenada cartesiana em polar usamos:

rho = sqrt(x^2 + y^2)

y = rho sin theta

Ou seja, podemos substituir a relação:

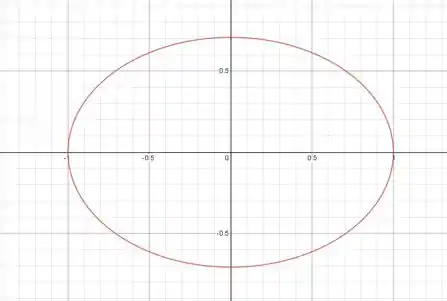
(rho^2 + rho^2 sin^2 theta) = 1 -> [(sqrt(x^2 + y^2))^2 + (y)^2] = 1 -> (x^2 + 2 y^2) = 1

Conhecemos essa relação e sabemos que é uma elipse com eixo maior valendo 1 e eixo menor valendo (1)/(sqrt(2))

Passo 2

Conhecemos essa relação e sabemos que é uma elipse com eixo maior valendo 1 e eixo menor valendo (1)/(sqrt(2))

Passo 3

A figura fica assim:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7-18 Esboce a região englobada pelas curvas e encontra a área12. x 2 = y , x = y - 2
7-18 Esboce a região englobada pelas curvas e encontra a área17. y = 2 + x - 1 , y = - 1 5 x + 7
7-18 Esboce a região englobada pelas curvas e encontra a área8. y = x 3 - 4 x , y = 0 , x = 0 , x = 2
7-18 Esboce a região englobada pelas curvas e encontra a área15. y = 2 x 2 + 1 , y = x
19-26.Use um recurso gráfico computacional, quando necessário, para encontra a região englobada pelas curvas.20. y = x 3 - 2 x 2 ,y = 2 x 2 - 3 x