Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.1 - Ex. 34
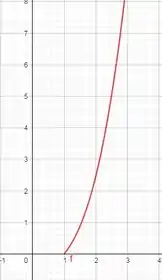
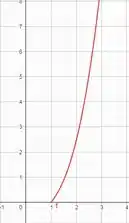
- Desenhe a curva
- Encontre a função comprimento do arco para essa curva com o ponto inicial
- Desenhe a função comprimento de arco
Passo 1
Muito bem, na letra a precisamos somente de desenhar a função com valores de x positivos.
Simples, não é? Então bora começar:
Na letra b queremos a função do comprimento do arco s(x), mas antes vamos achar:
Se a nossa função g é:
A sua derivada é:
Na raiz:
Para conseguirmos tirar o termo da nossa raiz, vamos transformar novamente em quadrado perfeito.
Bem fácil neste caso, certo?
Pronto ! Agora podemos achar nossa função.
Passo 2
Vamos lembrar como é a função do arco?
Só tivemos uma mudança da variável x para a t. Sendo assim:
Até aqui tudo tranquilo. Quanto aos intervalos vamos do x do ponto inicial até um ponto qualquer:
Tiramos as constantes:
E agora podemos resolver:
Aplicando o intervalo:
Sendo assim, a função arco é:
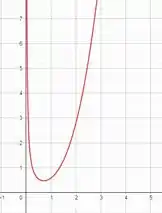
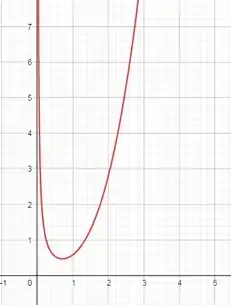
Passo 3
Nós já temos uma função, então vamos desenhar !
