Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.1 - Ex. 21
Trace a curva e estime visualmente seu comprimento. A seguir, encontre seu comprimento exato.
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que estimar visualmente e calcular o comprimento da curva
No intervalo
Parece complicado?
Primeiro podemos esboçar o gráfico de no intervalo e assim estimar seu comprimento usando algum método básico.
Já para calcular seu valor exato, fazemos
Onde e são as extremidades do intervalo de .
Veja só!
Passo 2
Primeiro a gente estima visualmente:
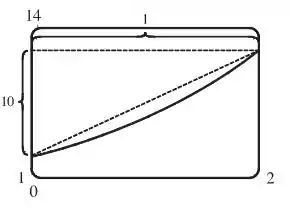
Pela figura, o comprimento da curva é suavemente mais largo que a hipotenusa do triângulo formado pelos pontos , , e .
Esse comprimento é mais ou menos , então nós devemos estimar o comprimento para ser .
Show?
Passo 3
Calculando a derivada de , temos
Dessa forma...
Então,
E aí! entendeu tudo? Responde Aí!
Resposta
.