Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.5 - Ex. 1d
Calcule o comprimento do gráfico da função dada.
d)
Passo 1
Para calcular o comprimento do gráfico, tudo que precisamos é encontrar os parâmetros da seguinte equação.
Do próprio enunciado, temos que , .
Calculando a derivada de
Montando a integral,
Agora é só calcular!
Passo 2
Aplicando a formula do comprimento:
Para que possamos resolver essa integral precisaremos fazer algumas substituições trigonométricas, para isso usaremos o triângulo abaixo para servir de norte!
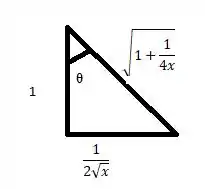
Do triângulo tiramos que:
Derivando dos dois lados teremos
Isolando :
Note também que:
Agora que já temos todas essas informações vamos reescrever a integral e calcular sua primitiva:
Lembrando que,
Colocando o para fora da integral:
Agora vamos resolver essa integral,
Passo 3
Usaremos o método da substituição por partes para calcular essa primitiva, lembrando que ao escolher bem e , facilita as contas!!!
Substituindo, teremos que:
Usando que :
Resolvendo, acharemos que:
Como , então:
Show, resolvemos a integral indefinida, mas fizemos isso em função de precisamos agora trocar essas funções trigonométricas por !
Mas eii! Nós já calculamos esses caras lembra?
Assim após a substituição ficaremos com:
Passo 4
Agora que já temos a faca e o queijo na mão, calcularemos o comprimento aplicando os limites de integração.
Só lembrando,
Substituindo o resultado da integral,
Logo,
Esperaaa um pouco, my friend, eu sei que parece que já acabou mais a resposta ainda pode ser melhorada se nos usarmos as propriedades básicas de logaritmo!