Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 1h
1 - Desenhe as curvas de nível e esboce o gráfico.
G -
Passo 1
Bem, sabemos que uma curva de nível pode ser encontrada fazendo . Nesse caso...
Tenha em mente que é sempre constante! De modo que...
Repare que essa equação representa retas constantes e paralelas ao eixo , já que ela deixa livre!
Mas atenção! As curvas de níveis de fato serão retas paralelas ao eixo , mas devem satisfazer essas condições aqui:
As duas primeiras inequações significas que devemos ter apenas o primeiro quadrante ativo. Já a terceira, significa que devemos estar sempre abaixo da reta :
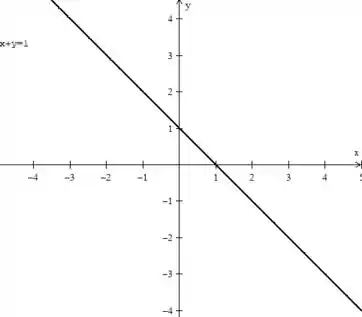
Então as nossas curvas de níveis (retas paralelas ao eixo ) devem estar dentro daquele triangulozinho! Veja algumas curvas de níveis:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-4, encontre o domínio e a imagem da função dada e identifique suas curvas de nível. Esboce uma curva de nível típica. g x , y = x 2 - y
Nos Exercícios 5-8, encontre o domínio e a imagem da função dada e identifique suas superfícies de nível. Esboce uma curva de nível típica. k x , y , z = 1 x 2 + y 2 + z 2 + 1
Nos Exercícios 1-4, encontre o domínio e a imagem da função dada e identifique suas curvas de nível. Esboce uma curva de nível típica. g x , y = 1 x y
Nos Exercícios 1-4, encontre o domínio e a imagem da função dada e identifique suas curvas de nível. Esboce uma curva de nível típica. f x , y = e x + y
Nos Exercícios 5-8, encontre o domínio e a imagem da função dada e identifique suas superfícies de nível. Esboce uma curva de nível típica. h x , y , z = 1 x 2 + y 2 + z 2