Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 1i
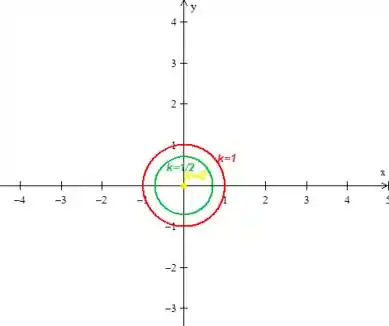
1 - Desenhe as curvas de nível e esboce o gráfico.
I -
Passo 1
Bem, sabemos que uma curva de nível pode ser encontrada fazendo . Nesse caso...
Elevando o quadrado...
CARA! O que é isso aí? SIMMMM!
Como é sempre constante, são circunferências!
Passo 2
Claro, como é constante, para cada valor de , teremos uma circunferência de raio diferente!
Vamos desenhar algumas delas aqui então:
Para , e :
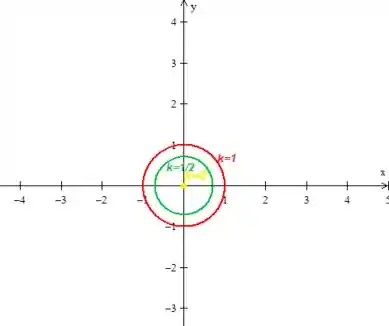
Resposta
Exercícios de Livros Relacionados
Use um computador para traçar o gráfico da função utilizando vários pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, trace o mapa
Use um computador para traçar o gráfico da função utilizando vários pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, trace o mapa
Use um computador para traçar o gráfico da função utilizando vários pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, trace o mapa
Use um computador para traçar o gráfico da função utilizando vários pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, trace o mapa
Nos Exercícios 5-8, encontre o domínio e a imagem da função dada e identifique suas superfícies de nível. Esboce uma curva de nível típica. g x , y , z = x 2 + 4 y 2 + 9 z 2