Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios adicionais e avançados - Ex. 28

  1. Desenhe a espiral hiperbólica r θ = 1. O que parece acontecer a ψ conforme a espiral gira ao redor da origem?
  2. Confirme seu achado no item (a) analiticamente.

Passo 1

Fala minha galera querida!! Vamos para mais um, estamos quase acabando os adicionais e avançados.

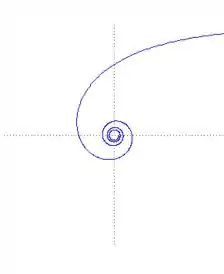  1. Vamos desenhar a curva,

    2. É difícil perceber com o desenho, mas o ângulo tangente vai se aproximando a ser 90°, vamos provar no item b.

    Passo 2

  2. Bora encontrar o limite da função tangente para confirmar o que percebemos.

r θ = 1

d r d θ = - θ - 2

t g   ψ = r r ' θ = 1 θ - θ - 2

t g   ψ = - θ

Agora podemos calcular o limite,

lim θ → ∞ ⁡ t g   ψ = - ∞

O único valor para a tangente ser infinita é 90°,

ψ = π 2

Está comprovado que o ângulo da tangente se aproxima de 90 graus.

Bora pro próximo.

Resposta

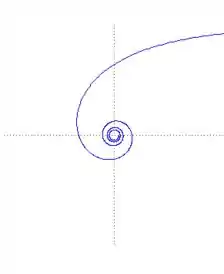
  2. ψ = π 2 , ângulo da tangente se aproxima de 90 graus.

Exercícios de Livros Relacionados

Encontre equações paramétricas para a curva dada.a ) R e t a p a s s a n d o p o r ( 1 , - 2 ) c o m c o e f i c i e n t e a n g u l a r 3 . b ) (x - 1)^2 + (y + 2)^2 = 9 c ) y = 4 x^2 - x d ) 9 x^2 +
Encontre equações paramétricas e um intervalo de parâmetro para o movimento de uma partícula que parta no ponto (-2, 0) no plano xy e trace o círculo x2 + y2 = 4 três vezes em sentido horário. (Existe
Encontre o valor de t g psi para a curva r = s e n^4 ((theta)/(4)) .
Mostre, por referência a uma figura, que o ângulo β entre as tangentes a duas curvas em um ponto de intersecção pode ser encontrado a partir da fórmula: t gβ = t gψ 2 - t gψ 1 1 + t g ψ 2t gψ 1 Quando
Encontre o ângulo no qual a cardioide r = a(1 - cos θ ) cruza o raio θ = π /2.