Desenhe os gráficos de e de .
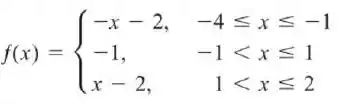
Passo 1
Fala, galera! Vamos fazer o seguinte:
- Vamos montar o gráfico da ;
- Vamos achar a ;
- Vamos montar o gráfico da .
Beleza?
Passo 2
O gráfico da nossa função é esse aqui:
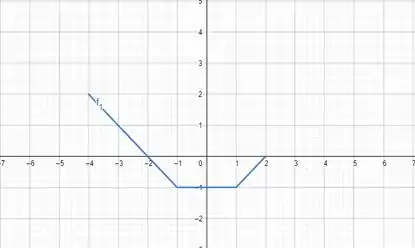
Passo 3
Pra montar o gráfico da composta, a gente vai fazer o seguinte: pegar o domínio da pra cada intervalo, achar a imagem e usar ela como o domínio da composta pra poder achar a imagem dela e montar o gráfico. QUÊ? Calma, vou te explicar enquanto eu faço:
Intervalo do domínio da que eu vou pegar: [-4,-1]
Mas vamos quebrar esse intervalo em dois: o de [-4,-3] e o de [-3,-1]
O [-4,-3] leva em que intervalo de ? No .
Então o (1,2] vai virar o meu .
Pra fazer a composta, vamos trocar ali em cima na função o pelo .
Onde que o (1,2] tá, na função ali em cima? Ele tá onde vale
O [-3,-1] leva em que intervalo de ? No (-1,1]
Então o (-1,1] vai virar o meu .
Pra fazer a composta, vamos trocar ali em cima na função o pelo .
Onde que o (-1,1] tá, na função ali em cima? Ele tá onde vale -1
Intervalo do domínio da que eu vou pegar: (-1,1]
Esse intervalo leva em que valor de ? No -1.
Então o -1 vai virar o meu .
Pra fazer a composta, vamos trocar ali em cima na função o pelo .
Onde que o -1 tá, na função ali em cima? Ele tá onde vale
Jogando -1 em , fica
Intervalo do domínio da que eu vou pegar: (1,2]
Esse intervalo leva em que intervalo da imagem? No .
Então o [-1,0] vai virar o meu .
Pra fazer a composta, vamos trocar ali em cima na função o pelo .
Onde que o [-1,0] tá, na função ali em cima? Ele tá onde vale -1.
Passo 4
Então, nosso gráfico vai ser assim:
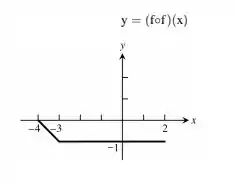
Resposta
Ei, a resposta está no passo a passo :)