Imagine um cabo, como de telefone ou de TV, preso por dois suportes e solto entre eles. O peso do cabo por unidade de comprimento é uma constante , e a tensão horizontal em seu ponto mais baixo é um vetor de comprimento .
Se adotarmos um sistema cartesiano para o plano do cabo no qual o eixo seja horizontal, a força da gravidade aponta para baixo, o eixo positivo aponta para cima e o ponto mais baixo do cabo está em no eixo (veja a figura a seguir), então é possível mostrar que o cabo acompanha o gráfico do cosseno hiperbólico
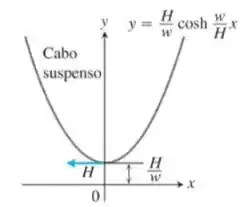
Às vezes, essa curva é denominada curva da corrente ou catenária; esse último termo vem do latim catena, que significa "corrente"
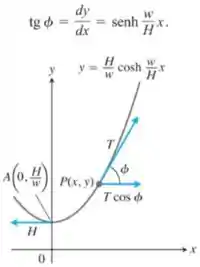
- Seja um ponto arbitrário no cabo. A figura a seguir mostra a tensão em P como um vetor de comprimento (magnitude) T, bem como a tensão em seu ponto mais baixo A. Demonstre que o coeficiente angular do cabo em P é
- Usando o resultado obtido no item (a) e o fato de que a tensão horizontal em P deve ser igual a H ( o cabo não está em movimento), demonstre que . Isso significa que a magnitude da tensão em é exatamente igual ao peso de y unidades do cabo.
Passo 1
- Vamos calcular a derivada da função
- A tensão em P é dada por
Considerando a variável . Os outros termos são constantes...
Como queríamos mostrar, o coeficiente angular é dado por
Passo 2
Vamos usar a identidade trigonométrica e fazer:
Agora a gente substitui pelo valor encontrado no item anterior...
E isso resulta em...
Agora a gente faz uma manipulaçãozinha...
E como
Chegamos em:
Como queríamos demonstrar.
Resposta
Ei, a resposta está no passo a passo :)