Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.4 - Ex. 1e
Dê os domínios e esboce os gráficos de e
e
Passo 1
Para achar basta somar as duas fuções para cada resrtrição de seus domínios:
Para :
Para :
Como o valor de f é o mesmo para qualquer número (racional ou não), é qualquer valor real, então sei domínio é:
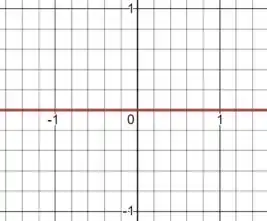
Então seu grafico é representado pela reta que corresponde ao eixo :
Passo 2
Para achar basta dividir as duas fuções:
Para cada restrição temos:
Para :
Para :
O domínio então é:
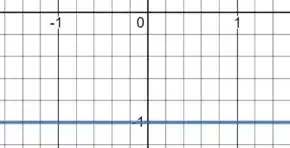
E seu gráfico é a reta :
Resposta
e
Exercícios de Livros Relacionados
Encontre as funções (a) fog , (b) gof , (c) fof , (d) gog , e seus domínios f x = x , g x = 1 - x 3
Encontre as funções (a) fog , (b) gof , (c) fof , (d) gog , e seus domínios
Encontre fogoh
Expresse a função na forma fog u t = tg t 1 + tg t
Expresse a função na forma f o g