Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.4 - Ex. 3c
Determine o “maior” conjunto tal que ; em seguida, construa a composta
e ,
Passo 1
Primeiramente devemos estabelecer o domínio de e a partir dessa restrição achar a imagem de
Repara que é uma raiz quadrada,
Se temos uma raiz quadrada, então não podemos ter números negativos dentro dela, logo:
Isso significa que o domínio de é dado por:
Passo 2
Então, a imagem de deve estar contida nesse intervalo.
Substituindo,
Fazendo o m.m.c.
Logo,
Fazendo o estudo de sinal:
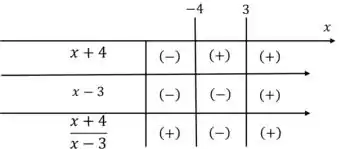
Então, temos que para ou .
Mas, no entanto, apresenta uma razão de duas funções, então seu denominador deve ser diferente de zero, ou seja,.
Desse modo, o conjunto que é o domínio de é dado por:
Passo 3
A composta é dada por:
Substituindo a expressão para
Agora vamos substituir
Ajeitando,
Resposta
e
Exercícios de Livros Relacionados
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O domínio de f ∘ g consiste em todos os valores de x no domínio de g nos quais g x ≠ 0 .
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O gráfico de uma função par é simétrico em relação ao eixo y .
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O gráfico de y = f x + 2 + 3 é obtido transladando o gráfico de y = f ( x ) duas unidades para a direita e três para cima.
Use a tabela do exercício 47 para resolver as equações f g x = 0 e g f x = 0
Encontre f x + h - f ( x ) h E f w - f ( x ) w - x E simplifique tanto quanto possível. f x = 3 x 2 - 5