Desenhe os gráficos dos conjuntos de pontos cujas coordenadas polares satisfaçam as equações e desigualdades nos Exercícios 11-26.
,
Passo 1
Fala minha galera querida!! Nesse exercício precisamos relembrar das equações polares definidas no eixo cartesiano.
Elas são:
Portanto, precisamos substituir os valores limites das desigualdades, e encontrar a área de intersecção. Vamos utilizar o Geogebra para nos ajudar.
Passo 2
Primeiro de tudo, vamos encontrar as funções e plotar todos os gráficos.
Para o raio temos:
Elevando todos os termos ao quadrado e substituindo:
E para os ângulos temos:
e
Porém, o ângulo não existe para tangente, então teremos que analisar de outra forma.
Passo 3
Vamos desenhar utilizando nosso querido Geogebra:
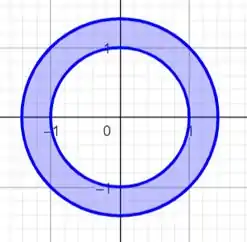
Temos esse arco circular, agora definiremos os ângulos, mas como?
Bom, sabemos que a primeira delimitação é que o ângulo deve ser menor do que , isto é, 90°, até alcançar o eixo x, que é a reta delimitada pela equação .
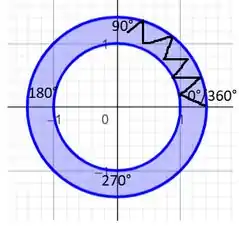 Então uma parte do arco é essa:
Então uma parte do arco é essa:
Já a outra delimitação, é que deve ser menor que , ou seja, deve ser menor do que , até chegar ao eixo x, que é a reta representada pela equação da tangente como já sabemos.
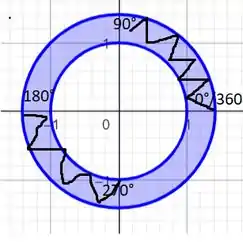
Passo 4
Então bora redesenhar já delimitando as intersecções, pois agora temos todas.
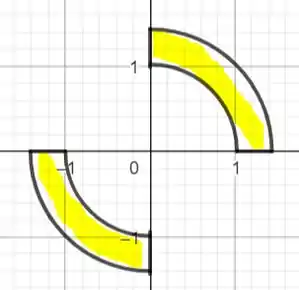
Portanto, essa é a nossa figura que respeita as desigualdades enunciadas.
Bora pro próximo.
Resposta
Ei, a resposta está no passo a passo :)