Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 36

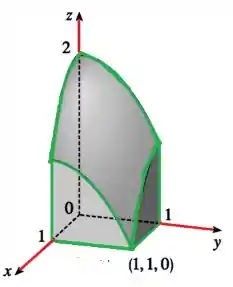
Desenhe o sólido cujo volume é dado pela integral iterada.

∫ 0 1 ∫ 0 1 2 - x 2 - y 2 d y d x

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O objetivo da questão é esboçar o sólido cujo volume é especificado pela integral:

∫ 0 1 ∫ 0 1 2 - x 2 - y 2 d y d x

Analisando os limites de integração, temos a região que delimita o sólido:

R : 0 ≤ x ≤ 1 ,   0 ≤ y ≤ 1

A função em questão é:

f x , y = 2 - x 2 - y 2

Podemos chamar f ( x , y ) de z . Portanto:

z = 2 - x 2 - y 2

Passo 2

Certo... Para descobrir como o paraboloide se comporta podemos considerar algumas situações.

Considerando x = 0 , temos:

2 - 0 2 - y 2 = z

z = 2 - y 2

Essa equação representa uma parábola no plano y z , veja o esboço a seguir:

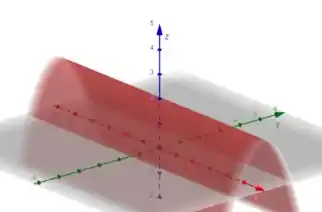
Considerando y = 0 , temos:

2 - x 2 - 0 = z

z = 2 - x 2

Que também representa uma parábola no plano z x , veja o esboço a seguir:

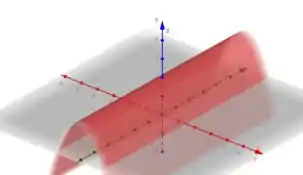
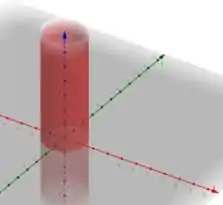
Considerando z = 0 , temos

z = 2 - x 2 - y 2

0 = 2 - x 2 - y 2

2 = x 2 + y 2

Que representa um círculo no plano x y , veja o esboço abaixo:

Passo 3

Agora que conhecemos os esboços dos gráficos nos planos x y , x z e y z podemos fazer um esboço tridimensional.

Porém precisamos respeitar os limites da região:

R : 0 ≤ x ≤ 1 ,   0 ≤ y ≤ 1

Fazendo isso teremos o seguinte sólido,

Resposta

E s b o ç o   d o   P a s s o   3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular o volume dos sólidos delimitados pelas superfícies dadas. 4 .x 2 + y 2 = 1 ,z = 0 e z = x 2 + y 2
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 7 .z = 9 - x 2 - y 2 e z = x 2 + y 2
Calcular o volume do no 1º octante, delimitado por z = 1 - 2 x - 3 y e os planos coordenados.
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 5 .x 2 + y 2 = 4 ,y + z = 8 e z = 0
Calcular o volume dos sólidos delimitados pelas superfícies dadas. 9 .x 2 + y 2 = 4 e z 2 + x 2 = 4