Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 45

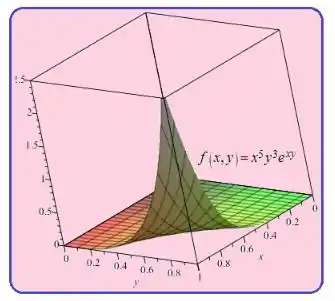
Use um sistema algébrico computacional para encontrar o valor exato da integral ∬ R x 5 y 3 e x y d A , onde R = 0,1 × 0,1 . Então use um CAS para desenhar o sólido que é dado pela integral.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Quando integramos:

∬ R x 5 y 3 e x y d A

Na região:

R = 0,1 × 0,1

i n t i n t x 5 ⋅ y 3 ⋅ e x ⋅ y ,   x = 0 . . 1 , y = 0 . . 1

A partir de um CAS, obtemos a resposta:

∬ R x 5 y 3 e x y d A = 21 e - 57

Passo 2

Para plotar também é fácil... Só inserir os parâmetros do enunciado e obtemos:

p l o t 3 d x 5 ⋅ y 3 ⋅ e x ⋅ y ,   x = 0 . . 1 , y = 0 . . 1

Resposta

∬ R x 5 y 3 e x y d A = 21 e - 57

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do conjunto dado.{ (x , y , z) in R^3 | 0 = x = 1 , 0 = y = 1 , 0 = z = x y e^(x^2 - y^2) }
Calcule o volume do conjunto dado.{ (x , y , z) in R^3 | 0 = x = 1 , 0 = y = 1 , 0 = z = x + 2 y }
Calcule o volume do conjunto dado.{ (x , y , z) in R^3 | 0 = x = 2 , 1 = y = 2 , 0 = z = sqrt(x y) }
Calcule o volume do conjunto dado.
Calcule o volume do conjunto dado.