Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.1 - Ex. 8
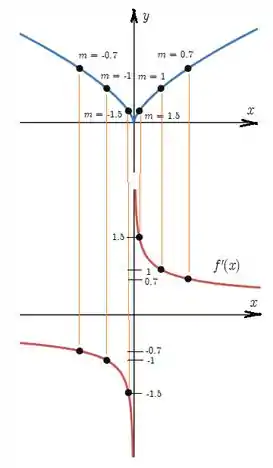
Trace ou copie o gráfico da função dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo para esboçar o gráfico de .
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Antes de tudo, você deve ir ao Exemplo 1 e entende-lo para que possa dar prosseguimento a atividade.
Nessa questão devemos traçar o gráfico de , ou seja, da derivada de , a partir do gráfico de que é esse aqui:
Primeiro, quando tiver uma tangente que seja horizontal, vamos ter uma intercessão no eixo no gráfico de . Nesse caso,não temos nenhuma tangente horizontal em , portanto não irá interceptar o eixo .
Agora vamos procurar por qualquer pontas no gráfico de , se tiver, haverá uma descontinuidade no gráfico de , aqui temos uma quina ali em .
Passo 2
Em qualquer intervalo em que tenha uma tangente com inclinação positiva, o gráfico de será positivo, e com inclinação negativa, o gráfico de será negativo, e se o gráfico da função for linear, o gráfico de será uma linha horizontal.
Vemos que aqui, da esquerda para a direita, o gráfico de tem inclinação negativa no segundo quadrante e inclinação positiva no primeiro quadrante.
O gráfico da derivada está ali embaixo da resolução. A ideia aqui é que vc leia osmotivos que me fizeram traçar um gráfico com aquela forma e entenda o por quê. No meu gráfico eu tracei os valores de que são as inclinações das retas tangentes e portanto os valores da derivada em cada ponto.
Podemos reparar que a medida que cresce e se aproxima de pela esquerda, a inclinação negativa se torna cada vez mais íngreme o que indica que a derivada será negativa com valor absoluto cada vez maior, tendendo ao infinito negativo quando chegar próximo a quina em .
E também reparamos que para maior que , no primeiro quadrante, a inclinação é positiva e aumenta a medida que tende a zero pela direita. Dessa forma, a derivada é positiva e aumenta seu valor cada vez mais ao se aproximar de zero, tendendo ao infinito positivo quando chega próximo a quina em .
Por fim, nas extremidades do gráfico de , vemos que a inclinação se torna quase que constante, pois a função se aproxima a uma reta a medida que tende a menos infinito e mais infinito. Dessa forma, a sua derivada será uma reta horizontal positiva para tendendo a infinito positivo e uma reta horizontal negativa para tendendo a infinito negativo.
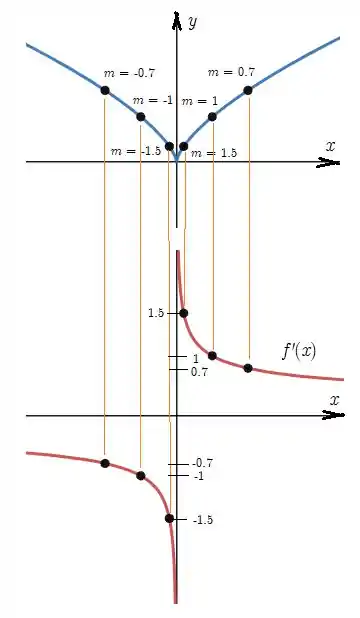
Resposta
