Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.7 - Ex. 16

O deslocamento (em metros) de uma partícula movendo-se ao longo de uma reta é dado pela equação

s = t 2 - 8 t + 18

Onde t é medido em segundos.

(a) Encontre as velocidades médias sobre os seguintes intervalos de tempo

  1. [ 3 ; 4 ]
  2. [ 3,5 ; 4 ]
  3. [ 4 ; 5 ]
  4. [ 4 ; 4,5 ]

(b) Encontre a velocidade instantânea quando t = 4 .

(c) Faça o gráfico de s em função de t e desenha as retas secantes cujas inclinações são as velocidades médias da parte (a), e a reta tangente, cuja inclinação é a velocidade instantânea da parte (b)

Passo 1

Fala aí, galerinha! 😬

Nesse problema foi dada uma equação que descreve o deslocamento de uma partícula em função do tempo

s = t 2 - 8 t + 18

A partir dessa equação queremos determinar as velocidades medias entre 3 ; 4 , [ 3,5 ; 4 ] , [ 4 ; 5 ] e [ 4 ; 4,5 ] .

Além disso queremos obter a velocidade instantânea em t = 4 s e tambem o gráfico de s .

Parece complicado? 🤔

Para calcular as velocidades medias, vamos fazer

v m = ∆ s ∆ t

E para obter a velocidade instantânea, vamos usar a definição de derivada

v = lim h → 0 ⁡ f a + h - f a h

Veja só! 👀

Passo 2

  1. Inicialmente, iremos calcular a posição da partícula nos seguintes instantes
  1. t = 3

    2. s 3 = 3 2 - 8 ⋅ 3 + 18 = 3 m

  2. t = 3,5

    3. s 3,5 = 3,5 2 - 8 ⋅ 3,5 + 18 = 2,25 m

  3. t = 4

    4. s 4 = 4 2 - 8 ⋅ 4 + 18 = 2 m

  4. t = 4,5

    5. s 4,5 = 4,5 2 - 8 ⋅ 4,5 + 18 = 2,25 m

  5. t = 5

s 5 = 5 2 - 8 ⋅ 5 + 18 = 3 m

Tranquilo até aqui? 😎

Passo 3

  1. Agora, calcularemos as velocidades médias, sabendo que

    2. v m = ∆ s ∆ t

    1. 3   ,   4

      2. v m 1 = 2 - 3 4 - 3 = - 1 m / s

    2. 3,5   ,   4

      3. v m 2 = 2 - 2,25 4 - 3,5 = - 0,5 m / s

    3. 4   ,   5

      4. v m 3 = 3 - 2 5 - 4 = 1 m / s

    4. 4   ,   4,5

    v m 4 = 2,25 - 2 4,5 - 4 = 0,5 m / s

    Bacana, não é? 😉

    Passo 4

  2. Encontraremos a velocidade instantânea através da equação 2. Daí

v = lim h → 0 ⁡ f a + h - f a h

Temos então que:

f a = s a = a 2 - 8 a + 18

f a + h = s a + h = a + h 2 - 8 a + h + 18

Substituindo:

v = lim h → 0 ⁡ a + h 2 - 8 a + h + 18 - a 2 + 8 a - 18 h

Realizando o produto notável e a distributiva:

v = lim h → 0 ⁡ a 2 + 2 a h + h 2 - 8 a - 8 h - a 2 + 8 a h

Simplificando termos semelhantes:

v = lim h → 0 ⁡ h h + 2 a - 8 h

Simplificando o h :

v = lim h → 0 ⁡ h + 2 a - 8

Calculando o limite:

v = 2 a - 8

v t = 2 t - 8

v 4 = 0 m / s

Interessante... 😉

Passo 4

c)

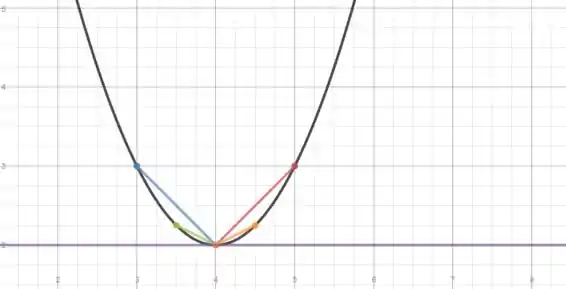
No gráfico abaixo vamos inserir os resultados que encontramos até aqui, veja que como o gráfico é s em função de t , s será nosso eixo vertical e t o horizontal. Além disso, veja que as retas estão localizadas nos seus respectivos pontos de posição e tempo em cada ponto.

Então se em t = 3 a posição é s = 3 , deveremos que plotar este ponto no gráfico e para o tempo t = 4 e a posição s = 2 do intervalo de tempo 3,4 vamos colocar esses dois pontos, ( 3,3 ) e ( 4,2 ) e ligá-los por uma reta.

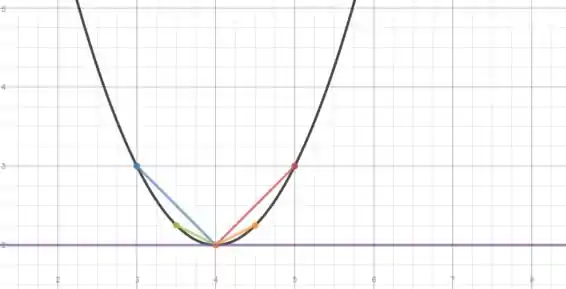
A curva preta é dada por (   s   =   t 2 –   8 t   +   18   )

A inclinação da secante azul é a velocidade média sobre o intervalo [ 3 ,   4 ] .

A inclinação da secante verde é a velocidade média sobre o intervalo [ 3.5 ,   4 ] .

A inclinação da secante vermelha é a velocidade média sobre o intervalo [ 4 ,   5 ] .

A inclinação da secante laranja é a velocidade média sobre o intervalo [ 4 ,   4.5 ] .

A linha reta roxa é a tangente em (   t   =   4   ) .

Observe que sua inclinação é zero, pois a velocidade é zero em (   t   =   4   ) .

E aí! o que achou? Responde Aí! 😁

Resposta

  1. v m 1 = - 1 m / s

    v m 2 = - 0,5 m / s

    v m 3 = 1 m / s

    v m 4 = 0,5 m / s

  2. v 4 = 0 m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule F^' (x) sendo F (x) igual ax e^x cos x
Calcule F^' (x) sendo F (x) igual a(1 + sqrt(x)) e^x tg x
Calcule F^' (x) sendo F (x) igual ae^x sen x cos x
Calcule f^' (x) .f (x) = x^2 ln x + 2 e^x
Seja f (x) = x^2 sen x + cos x . Calcule:f^' (x) f^' (0) f^' (3 a) f^' (x^2)