Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 160

Determinação da altura

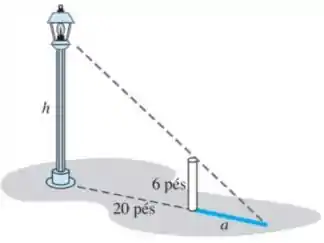
Para determinar a altura de um poste para iluminação (veja a figura), você coloca um mastro de 6   p é s na posição vertical a 20   p é s do poste e mede o comprimento da sombra, que é de 15   p é s , com um erro de mais ou menos uma polegada. Calcule a altura do poste usando

a = 15   p é s e estime o erro possível no resultado.

Passo 1

Observando o desenho dado pelo enunciado, podemos perceber que o poste e o mastro formam triângulos retângulos com o solo e, então, é possível utilizar relações métricas entre eles envolvendo a altura h e o comprimento da sombra a , tal que:

h 20 + a = 6 a

h = 120 a + 6  

E, portanto:

d h = - 120 a 2 d a = 120 a 2 d a

Além disso, o enunciado nos dá o erro do comprimento da sombra d a = 1   p o l = 0,08333   p é s .

Passo 2

Como foi pedido, podemos determinar a altura do poste utilizando a = 15   p é s :

h = 120 a + 6 = 120 15 + 6 = 14

E também podemos encontrar:

d h = 120 a 2 d a = 120 15 2 ( 0,0833 ) = 0,0444

Passo 3

Logo, com os dois últimos valores encontrados, podemos estimar o erro gerado ao calcular a altura do poste. Tal erro é dado por:

d h h = 0,0444 14 = 0,00317

Em termos de porcentagem:

d h h = 0,00317 100 % = 0,317 %

Resposta

A altura do poste é h = 14   p é s e o erro possível desse resultado é de 0,317 % .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma escada com 12m está apoiada em uma parede e faz um ângulo θ com o chão. Se o topo da escada está a uma altura de h m na parede, expresse h em termos de θ e então use d h para estimar a variação em
Um cubo de aço com 1 cm de lado é coberto com 0,01 cm de cobre. Use diferenciais para estimar o volume de cobre na cobertura. [sugestão: seha ∆ V a variação no volume do cubo).
A resitência elétrica R de um fio é dada por R = k r 2 , onde k é uma contante e r o raio do fio. Supondo que o raio do fio tenha um erro possível de ± 5 % , uso diferenciais para estimar o erro perce
A hipotenusa de um triângulo retângulo mede exatamente 10 cm, e um dos ângulos agudos mede 30 ° , com erro possível de ± 1 ° (a) Use diferenciais para estimar os erros nos lados opostos e adjacente ao
A área de um círculo é computado a partir do valor medido de seu diâmetro. Estime o máximo erro percentual possível na medida se o erro percentual na área deve ser mantido em não mais de ± 1 % .