Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 1.6 - Ex. 1h
Determinar todos os intervalos de um número que satisfaçam as desigualdades abaixo. Fazer a representação gráfica.
h)
Passo 1
Como a variável encontra – se no denominador da fração, é necessário analisar os casos onde as soluções são cabíveis. Não entendeu? O denominador não pode ser zero, então temos que trabalhar com valores que não zere o denominador, logo:
Primeiro caso:
Resolvendo a inequação e aplicando a solução acima:
Logo, não há que satisfaça essa inequação, já que o delta dá um valor negativo!
Segundo caso:
Resolvendo a inequação e aplicando a solução acima:
A solução para esse caso pertence ao conjunto dos números Irracionais!
Solução final caso 2:
Terceiro caso:
Resolvendo a inequação e aplicando a solução acima:
A solução para esse caso pertence ao conjunto dos números Irracionais!
Solução final caso 3:
Quarto caso:
E enfim a solução final real oficial será a intersecção das soluções encontradas!
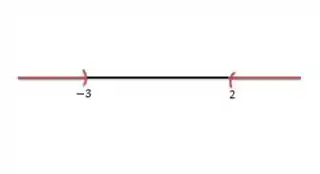
A representação gráfica será:
