Determinar todos os intervalos de um número que satisfaçam as desigualdades abaixo. Fazer a representação gráfica.
q)
Passo 1
Nesse caso, iremos “transformar” a equação em duas partes, então fica assim:
Como a segunda equação é redutível, temos
Agora vamos analisar, como temos duas equações, podemos usar a desigualdade.
Fazemos:
Portanto,
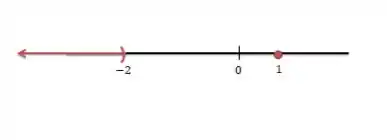
A solução final é: .
A representação gráfica será: