Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 1.6 - Ex. 1f

Determinar todos os intervalos de um número que satisfaçam as desigualdades abaixo. Fazer a representação gráfica.

f) x 2 - 3 x + 2 > 0

Passo 1

Inicialmente precisamos achar as raízes da equação, logo usaremos a formula de Báskara para isso:

x 2 - 3 x + 2 = 0

∆ = b 2 - 4 a c

x = - b   ± ∆ 2 a

∆ = ( - 3 ) 2 - 4 ( 1 ) ( 2 )

∆ = 1

x = - ( - 3 )   ± 1 2 ( 1 )

x = 1   e   x = 2

Como já conhecemos as raízes, voltamos a inequação:

x - 1 x - 2 > 0

x   ∄   [ 1,2 ]

A solução acima mostra que para valores entre 1 e 2 não é satisfeito a condição de ser maior que zero, logo valores antes de 1 e depois de 2 se forem aplicados na inequação vão dar um número maior que zero.

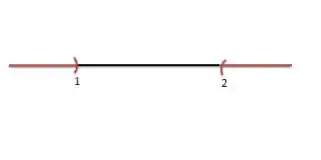
A representação gráfica será:

Resposta

x   ∄   [ 1,2 ]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o conjunto solução da desigualdade dada e mostre-o na reta numérica real x - 3 x + 50
Ache o conjunto solução da desigualdade dada e mostre-o na reta numérica real 2 ≤ 5 - 3 x11
Ache o conjunto solução da desigualdade dada e mostre-o na reta numérica real 4 x 2 + 9 x9
Ache o conjunto solução da desigualdade dada e mostre-o na reta numérica real 5 x + 2x - 6
Ache o conjunto solução da desigualdade dada e mostre-o na reta numérica real 3 - x5 + 3 x